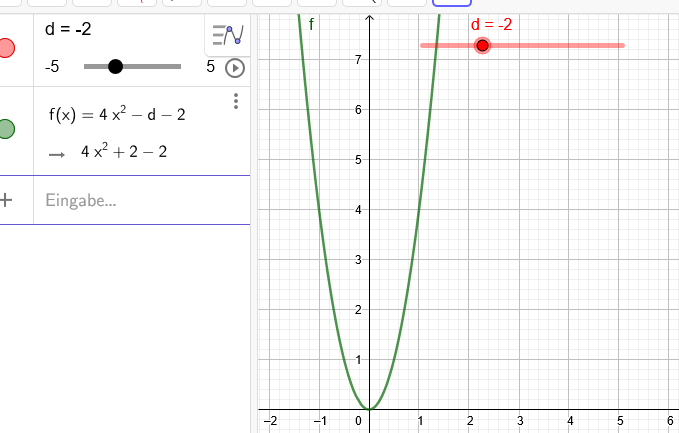
Gegeben ist die quadratische Gleichung in der Unbekannten x mit 4x^2 -d =2 . Geben Sie denjenigen Wert für d an, für den die Gleichungen genau eine reelle Lösung hat. Wie lautet diese Gleichung?
4x^2 -d =2 |+d
4x^2 =2+d |:4
x^2=\( \frac{2+d}{4} \)| \( \sqrt{} \)
Der Term unter der Wurzel muss 0 sein
\( \frac{2+d}{4} \)=0
d=-2
4x^2-(-2) =2
4x^2+2=2
4x^2=0