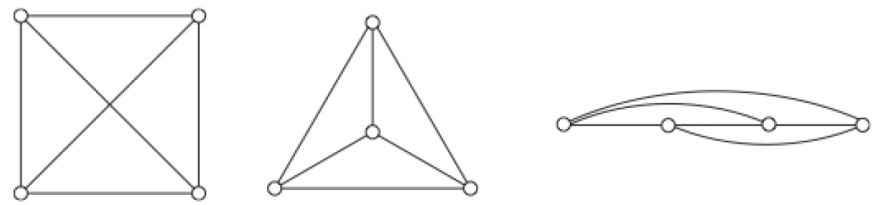
Zwei Graphen \( G, G^{\prime} \) mit gleichviel Ecken heissen isomorph (ununterscheidbar) wenn man ihre Ecken \( e_{1}, \ldots, e_{n} \) und \( e_{1}^{\prime}, \ldots, e_{n}^{\prime} \) beide so durchnummeriern kann, dass \( \left\{e_{i}, e_{j}\right\} \) genau dann eine Kante in \( G \) ist, wenn \( \left\{e_{i}^{\prime}, e_{j}^{\prime}\right\} \) eine Kante in \( G^{\prime} \) ist. Untersuchen Sie ob folgende Graphen mit 4 Ecken isomorph sind.