f(t)= 3*\( \sqrt{t} \) +\( \frac{2}{11} \)t +\( \sqrt[5]{t^3} \)
f(t)= 3*\( \sqrt{t} \) +\( \frac{2}{11} \)t +\( t^{0,6} \)
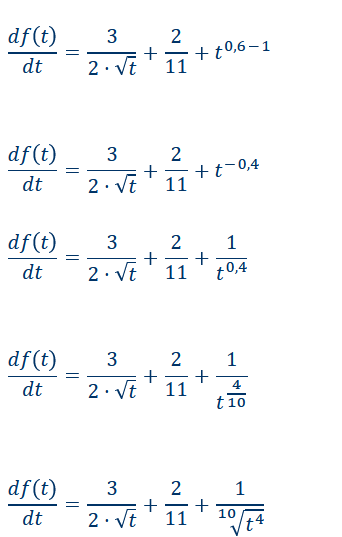
Text erkannt:
\( \frac{d f(t)}{d t}=\frac{3}{2 \cdot \sqrt{t}}+\frac{2}{11}+t^{0,6-1} \)
\( \frac{d f(t)}{d t}=\frac{3}{2 \cdot \sqrt{t}}+\frac{2}{11}+t^{-0,4} \)
\( \frac{d f(t)}{d t}=\frac{3}{2 \cdot \sqrt{t}}+\frac{2}{11}+\frac{1}{t^{0,4}} \)
\( \frac{d f(t)}{d t}=\frac{3}{2 \cdot \sqrt{t}}+\frac{2}{11}+\frac{1}{t^{\frac{4}{10}}} \)
\( \frac{d f(t)}{d t}=\frac{3}{2 \cdot \sqrt{t}}+\frac{2}{11}+\frac{1}{10} \sqrt{t^{4}} \)