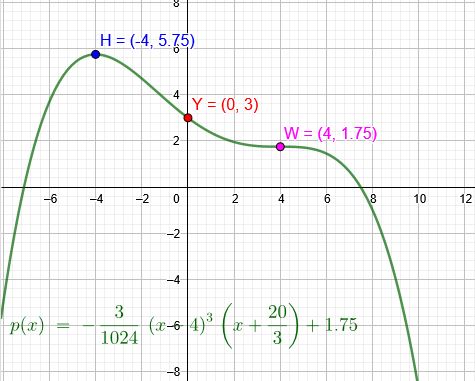
Der Graph einer ganzrationalen Funktion vierten Grades hat den Hochpunkt bei \(x =-4\) und den Wendepunkt W \((4|1,75)\) mit waagerechter Tangente. Der Graph schneidet die y-Achse bei \(y=3\).
Wendepunkt W \((4|\red{1,75})\) mit waagerechter Tangente.
Ich verschiebe um \(\red{1,75}\) Einheiten nach unten:
W \((4|\red{1,75})\) ↓ W´ \((4|0)\)
Hier ist nun eine Dreifachnullstelle:
\(f(x)=a[(x-4)^3(x-N)]\)
\(f'(x)=a[3(x-4)^2(x-N)+(x-4)^3 \cdot 1]\)
Hochpunkt bei \(x =-4\)→waagerechte Tangente :
\(f'(-4)=a[3(-4-4)^2(-4-N)+(-4-4)^3]=a[192(-4-N)-512]\)
\(a[192(-4-N)-512]=0\)
\(a[192(-4-N)-512]=0\) \(-1280 -192N=0\) \(N=-\frac{20}{3}\)
\(f(x)=a[(x-4)^3(x+\frac{20}{3})]\)
Der Graph schneidet die y-Achse bei \(y=3\) ↓ Y´\((0|1,25)\):
\(f(0)=a[(0-4)^3(0+\frac{20}{3})]=1,25\)
\(a[- \frac{1280}{3}]=\frac{5}{4}\)
\(a=-\frac{3}{1024}\)
\(f(x)=-\frac{3}{1024}[(x-4)^3(x+\frac{20}{3})]\) ↑
\(p(x)=-\frac{3}{1024}[(x-4)^3(x+\frac{20}{3})]+1,75\)