Aufgabe:
Hier sind die Vektoren \( \vec{a}, \vec{b}, \vec{c} \) und d gezeichnet.
Zeichnen Sie den Vektor und geben Sie seine Koordinaten an.
a) \( \vec{a}+\vec{b} ;-\vec{a}+\vec{b} ;-\vec{b}+\vec{a} \)
b) \( \vec{a}+\vec{b}+\vec{c} ; \vec{d}-\vec{a}+\vec{b} ; \vec{c}-\vec{d}-\vec{a} \)
c) \( (\vec{a}+\vec{b})-(\vec{c}+\vec{d}) ;(\vec{a}-\vec{b})+(\vec{c}-\vec{d}) \)
d) Bestimmen Sie zeichnerisch und rechnerisch den Vektor \( \vec{x} \) mit \( \vec{a}+\vec{c}+\vec{x}=\vec{d} \)
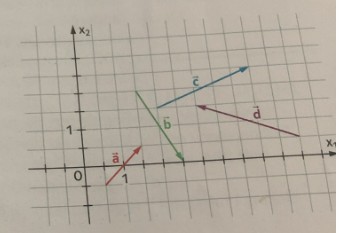
Problem/Ansatz:
Kann mir jemand bitte bei der d) erklären, wie ich den Vektor x zeichnerisch und rechnerisch ermitteln kann.