Hallo,
Sei qa der Berührpunkt zwischen cb, dann muss ja schonmal c=0 sein oder ?
wohl eher \(a=0\) - oder?
'ne Skizze ist auf jeden Fall von Vorteil:
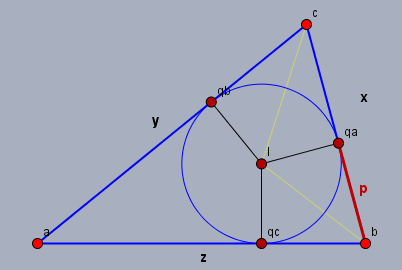
mal angenommen, das rot markierte Streckenstück sei \(|bq_a|=p\), dann ließe sich der Punkt \(q_a\) in Form einer Affinkombination schreiben als$$q_a = \frac px c + \frac{x -p}{x}b$$Setze \(p\) mal auf \(p=0\) bzw. \(p=x\), und prüfe, ob dies zu sinnvollen Ergebnissen führt.
Für die Berührpunkte des Inkreises gilt doch, wegen der Symmetrie zur jeweiligen Winkelhalbierenden:$$|q_cb| = |q_ab| \quad |q_ac| = |q_bc|\quad |q_ba| = |q_ca|$$und daraus folgt weiter$$y + p= \frac12(x + y + z) \\ \implies p = \frac12(x - y + z)$$und dies setzt man in die obige Gleichung für \(q_a\) ein:$$q_a = \frac 1x\left(\frac12(x - y + z)c + (x -\frac12(x - y + z))b\right) \\ \phantom{q_a} = \frac 1{2x}\left( (x - y + z)c + (x + y - z)b\right) \\ \phantom{q_a} = \left(\frac 12 - \frac{y - z}{2x}\right)c + \left(\frac 12 + \frac{y - z}{2x}\right)b$$Die Affinkombinationen für \(q_b\) und \(q_c\) erhält man über einen zyklischen Ringtausch von \(x\), \(y\) und \(z\) und \(a\), \(b\) und \(c\).
Gruß Werner