Hallo,
solange dies so eine einfache Figur mit einer (einfachen) 90°-Drehung ist, geht das auch ohne Rechnung. Ich unterstelle mal, dass das kleine Häuschen zu dem großen rechts transformiert werden soll.
Zeichne dazu im Originalbild die Einheitsvektoren (hier grün und blau) des Koordinatensystems ein.
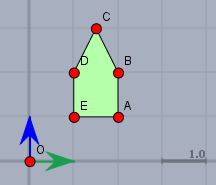
Und nun die 'gleichen' Vektoren im Zielbild. Mit 'gleich' ist aus der Sicht des transformierten Objekts gemeint. Das sollte hier so aussehen.
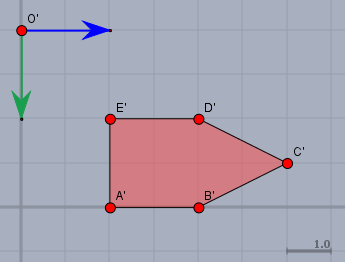
Und nun brauchst Du nur ablesen! Und zwar in den Koordinaten des Zielsystems. Der grüne Vektor und blaue Vektor im Zielbild sind$$e_x=\begin{pmatrix}0\\ -2\end{pmatrix}, \quad e_y=\begin{pmatrix}2\\ 0\end{pmatrix}$$ Und die Position des Ursprungs \(O'\) liegt bei $$p=\begin{pmatrix}0\\ 4\end{pmatrix}$$nur noch richtig hinschreiben:$$M = \left(\begin{array}{cc|c} e_x& e_y& p \\\hline 0& 0& 1\end{array}\right) = \begin{pmatrix}0& 2& 0\\ -2& 0& 4\\ 0& 0& 1\end{pmatrix}$$Kleine Denkaufgabe: es ginge auch mit $$e_x=\begin{pmatrix}0\\ 2\end{pmatrix}, \quad e_y=\begin{pmatrix}2\\ 0\end{pmatrix},\quad p=\begin{pmatrix}0\\ -2\end{pmatrix}$$Warum ist das auch nicht falsch? Und was ist da anders?
Wenn es komplexer wird, suchst Du Dir drei relevante Punkte im Originalsystem \((p_1,\,p_2,\,p_3)\) und Zielsystem \((q_1,\,q_2,\,q_3)\) und rechnest$$M = \begin{pmatrix}q_1& q_2& q_3\\ 1& 1& 1\end{pmatrix} \cdot \begin{pmatrix}p_1& p_2& p_3\\ 1& 1& 1\end{pmatrix}^{-1}$$Die Punkte im Originalsystem dürfen nicht auf einer Geraden liegen!
Das \(M\) steht genau dann für eine winkeltreue Abbildung, wenn seine beiden Vektoren aus den ersten Spalten senkrecht zueinander stehen und gleich lang sind.
Noch zu Deinen Fragen:
1) Verschiebt die Rotation das Objekt nicht nochmal aus dem Ursprung?
Ja, sobald die Rotationsmatrix bei der Multiplikation die erste ist. \(R \cdot T\) verschiebt den Ursprung und \(T \cdot R\) verschiebt ihn nicht. Das gleiche gilt für einen Skalierung.
2) Was muss ich beim Zusammenfassen der Matrizen beachten? Kann ich die einfach so ausmultiplizieren?
Gute Frage! man kann/soll nur das multiplizieren, was zusammen gehört. Hier musst Du sie rückwärts multiplizieren, da die Matrizen, die links stehen, ja zuerst 'wirken'. Also so$$T_1 = \begin{pmatrix}1& 0& -1\\ 0& 1& -1\\ 0& 0& 1\end{pmatrix}\\ S_1= \begin{pmatrix}2& 0& 0\\ 0& 2& 0\\ 0& 0& 1\end{pmatrix} \\ R_1 = \begin{pmatrix}0& 1& 0\\ -1& 0& 0\\ 0& 0& 1\end{pmatrix}\quad \to -90°\\ T_2=\begin{pmatrix}1& 0& 2\\ 0& 1& 2\\ 0& 0& 1\end{pmatrix}$$(ich habe den Punkt \(E\) links unten am Haus als Bezug gewählt!) und nun 'rückwärts' zusammen fassen$$M= T_2\cdot R_1\cdot S_1\cdot T_1 = \begin{pmatrix}0& 2& 0\\ -2& 0& 4\\ 0& 0& 1\end{pmatrix}$$Stelle dir einen Punkt des Originals vor. Dieser wird ja zuerst mit \(T_1\) multipliziert und danach erst mit \(S_1\) usw.
Da könnte man noch viel zu sagen, aber das soll zunächst reichen ;-)
Gruß Werner