Aufgabe:
Hallöchen,
Es geht um die Konstante C beim aufleiten, die beim unbestimmten Integral auftaucht. Jedoch verstehe ich die Formel die wir im Skript stehen haben einfach nicht. ( siehe Anhang )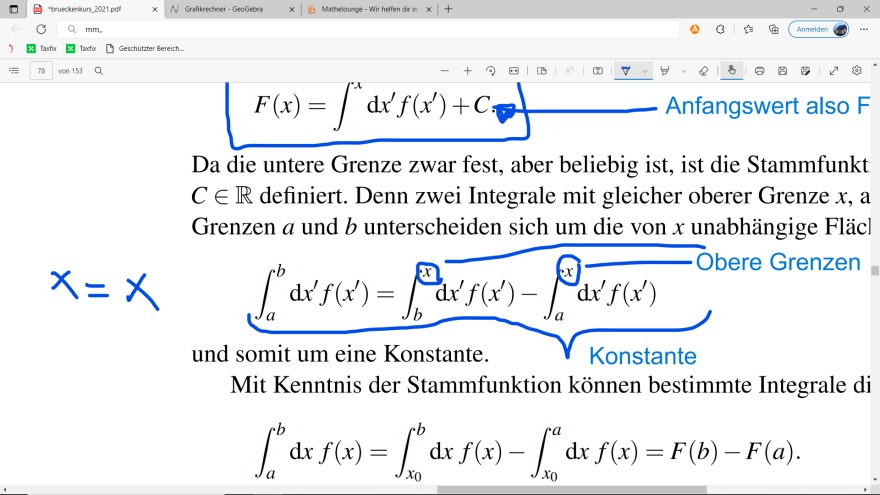
Text erkannt:
Da die untere Grenze zwar fest, aber beliebig ist, ist die Stammfunkt \( C \in \mathbb{R} \) definiert. Denn zwei Integrale mit gleicher oberer Grenze \( x \), a Grenzen \( a \) und \( b \) unterscheiden sich um die von \( x \) unabhängige Fläcl
\( \begin{array}{c} \int \limits_{a}^{b} \mathrm{~d} x^{\prime} f\left(x^{\prime}\right)=\int \limits_{b}^{x} \mathrm{~d} x^{\prime} f\left(x^{\prime}\right)-\int \limits_{a}^{x} \mathrm{~d} x^{\prime} f\left(x^{\prime}\right) \\ \text { und somit um eine Konstante. } \\ \text { Mit Kenntnis der Stammfunktion können bestimmte Integrale di } \\ \int \limits_{a}^{b} \mathrm{~d} x f(x)=\int \limits_{x_{0}}^{b} \mathrm{~d} x f(x)-\int \limits_{x_{0}}^{a} \mathrm{~d} x f(x)=F(b)-F(a) \end{array} \)
Es geht um die Formel in der Mitte.
Das linke Integral gibt Integrationsgrenzen an, wobei doch a < b sein sollte, damit diese Fläche nicht negativ wird.
Beim rechten Term, der Differenz der beiden Integrale mit gleicher oberer Grenze, müsste dann das x ( also die obere Grenze) größer als a und größer als b sein, also:
x>a
x>b
Mit dieser Vorgehensweise komme ich leider iwie nicht weiter und würde jede Hilfe begrüßen.