a) Den Flächeninhalt von dem Trapez bestimmt man wie gewohnt:
$$A_{Trapez}=\dfrac{(a+c)\cdot h }{2}$$
Nun zu den Variablen:
a entspricht dem Betrag Strecke BB'. Wegen Spitze minus Schaft gilt:
$$|\overline{BB'}|=\left|\left(\begin{matrix}1\\3\\3\end{matrix}\right)-\left(\begin{matrix}1\\-3\\3\end{matrix}\right)\right|=\left|\left(\begin{matrix}0\\6\\0\end{matrix}\right)\right|=6$$
c wiederum entspricht dem Betrag von AA':
$$|\overline{AA'}|=\left|\left(\begin{matrix}3\\2.5\\0\end{matrix}\right)-\left(\begin{matrix}3\\-2.5\\0\end{matrix}\right)\right|=\left|\left(\begin{matrix}0\\5\\0\end{matrix}\right)\right|=5$$
Und h entspricht dem Betrag der Strecke M_A und M_B. Dabei sei angemerkt, dass M_B in der Mitte von B und B', also bei (1|0|3) liegen muss:
$$|\overline{M_AM_B'}|=\left|\left(\begin{matrix}3\\0\\0\end{matrix}\right)-\left(\begin{matrix}1\\0\\3\end{matrix}\right)\right|=\left|\left(\begin{matrix}2\\0\\-3\end{matrix}\right)\right|=\sqrt{2^2+3^2}=\sqrt{13}\approx3.6$$
Wir setzen ein:
$$A_{Trapez}=\dfrac{(a+c)\cdot h }{2}=\dfrac{(6+5)\cdot\sqrt{13}}{2}\approx19.83\text{ m}^2$$
b) Die Neigung lässt sich am besten an der Strecke M_A und M_B bestimmen. An den Koordinaten lesen wir ab: Geht man zwei Meter nach hinten, steigt die Kletterwand um drei Meter an.
Die Steigung ist also 3/2. In Grad wandelt man eine Steigung mit dem Arkustangens (dir vielleicht unter tan^-1 bekannt). Wir setzen ein:
$$\arctan\left(\dfrac32\right)=\tan^{-1}\left(\dfrac32\right)\approx56.31$$
Die Kletterwand ist also zu steil.
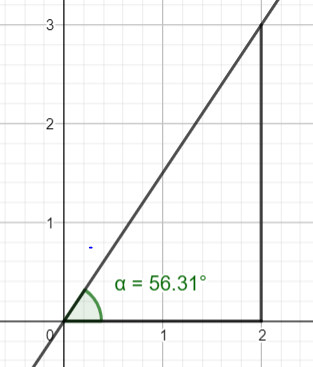
Die Kletterwand im Seitenprofil.
Ich hoffe, ich hab die Angabe richtig verstanden und mich nicht verrechnet.
LG