Graphen der Funktion f mit der Steigung

Question

Aufgabe:

Ein Anbieter für Outdoor-Aktivitäten möchte seine Kunden über die schönsten Mountainbike-Touren im Sauerland informieren. Dazu sollen auf einem Flyer alle wichtigen Merkmale der Touren zusammengefasst werden.
Mithilfe einer App hat er herausgefunden, dass sich das Höhenprofil der Tour mithilfe verschiedener Graphen modellieren lässt. Ein Tourabschnitt lässt sich auf dem Intervall [1; 10] vereinfacht durch den Graphen der Funktion f mit () = −0,754 + 173 − 1202 + 300 darstellen. Dabei gibt x die horizontale Entfernung (in km) und f(x) die zugehörige Höhe (in m) über NN an.

Problem/Ansatz:

Ich muss die Steigung berechnen habe aber keine Ahnung wie ich was machen muss und auch vorgehen muss. Kann mir jemand helfen

Comments

Überprüfe bitte deine Funktionsangabe. Da kommen sehr wenig \(x\) vor.

---

Stimmt tut mir leid

(f) = −0,75x^4 + 17x³ − 120x² + 300x

Answer 1

Aloha :)

Die Steigung berechnest durch Bildung der sog. Ableitung. Um \(x^n\) abzuleiten, holst du den Exponenten als Faktor vor den Term und verminderst danach den Exponenten um \(1\), d.h.:$$x^n\to n\cdot x^{n-1}$$Die Ableitung der Funktion$$f(x)=-0,75x^4+17x^3-120x^2+300x$$lautet daher:$$f'(x)=-0,75\cdot4x^3+17\cdot3x^2-120\cdot2x+300\cdot1x^0$$$$\phantom{f'(x)}=-3x^3+51x^2-240x+300$$

Comments

Was mache ich danach ?

---

Das ist die Steigung.

Wenn du einen Ort \(a\) in \(f'(x)\) einsetzt, erhältst du die Steigung am Ort \(a\).

---

Irgendwie versteh ich das nicht was ist den Ort a

---

Du hast geschrieben, dass du die Ableitung berechnen sollst.

Merke: Steigung = 1. Ableitung

Tschaka hat die 1. Ableitung gebildet.

Mit dem Ort/'Entfernung = a ist gemeint, wenn du die Steigung z.B. nach 4 km bestimmen sollst, setzt du 4 für x in die 1. Ableitung ein:

\(f'(4)=-3\cdot 4^3+51\cdot 4^2 -240\cdot 4+300=-36\)

Graphisch sieht das so aus:

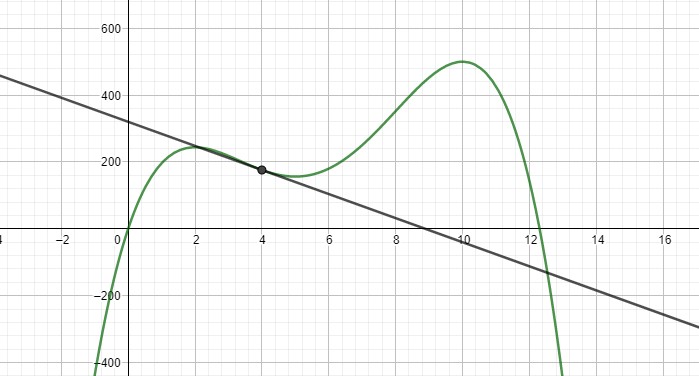Die Gerade, die den Punkt (4|176) berührt (= Tangente) hat die Steigung -36.

Somit kannst du die Steigung an jedem beliebigem Punkt/Ort bestimmen.