Strahlensatz und Gleichungssysteme um die Höhe des Wasserschlosses zu bestimmen

Question

Hallo Ihr Lieben,


hänge mal wieder an einer kniffligen Aufgabe, würde mich über sehr über Hilfe freuen :)




Aufgabe:







Paul möchte die Höhe eines unzugänglichen Wasserschlosses bestimmen. Dazu stellt er eine 3,50 m langen Stab so auf, dass die Schattenspitze des Turms und die des Stabes zusammenfallen (siehe Skizze). Er misst die einzige Strecke, die zugänglich ist und trägt sie in seiner Planfigur ein.
Beim Nachdenken über die mögliche Lösung wandert der Schatten des Schlosses.
Plötzlich fällt er genau auf den Punkt, an dem der Stab im Boden steckt.
Paul muss nun den Stab genau um 12.30 m versetzen, um die ursprüngliche Situation wiederzuerhalten. (Beide Schatten fallen aufeinander.)



1. Zeichne eine Planfigur, die dieses Sachverhalt beschreibt und trage alle bekannten Streckenlängen ein.

2. In welcher Tageshälfte hat Paul seine Messung vorgenommen?
    Wie muss Paul vorgehen, wenn er das Problem in der anderen Tageshälfte lösen wollte?

3. Berechne die Höhe des Wasserschlosses.






 

Answer 1

Skizze:

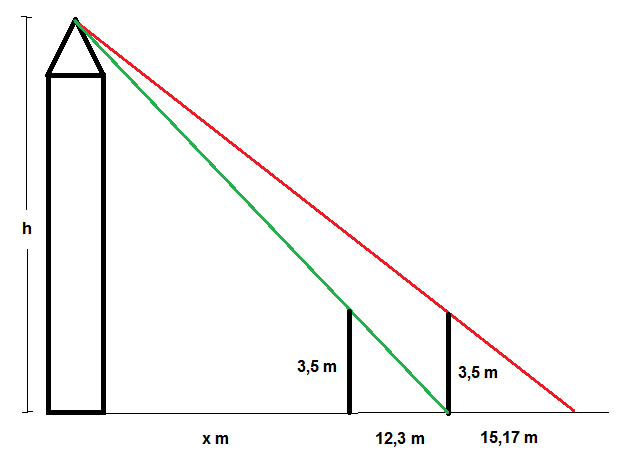
Da der Schatten des Schlosses kürzer geworden ist, muss die Sonne gestiegen sein, Paul hat seine Messungen also am Vormittag vorgenommen. 

Wollte er Nachmittags messen, dann müsste er vor allem zunächst auf die andere Seite des Schlosses gehen, weil der Schatten des Schlosses dann dort zu finden wäre.

c) Berechnung der Höhe

Nach Strahlensatz gilt:

15,17 / 3,5 = ( 15,17 + 12,3 + x ) / h

und

12,3 / 3,5 = ( 12,3 + x ) / h

Löst man dieses Gleichungssystem auf, so erhält man:

h = 18,5 m (genau!)

x ≈ 52,71 m

Die Höhe des Schlosses beträgt also 18,5 m.

Answer 2

Wir stellen ein Gleichungssystem auf

h / x = 3.5 / 15.17
15.17h = 3.5x
15.17h - 3.5x = 0

h / (x - 15.17) = 3.5 / 12.3
12.3h = 3.5(x - 15.17)
12.3h = 3.5x - 53.095
12.3h - 3.5x = - 53.095

Die Lösung des Gleichungssystems ist
x = 56129/700 ∧ h = 37/2
x = 80.18428571 ∧ h = 18.5

Eine Schlosshöhe von 18.5 m erscheint mir etwas gering

Da der Schatten kürzer wird muss die Messung am Morgen vorgenommen worden sein.

Du kannst dir ja mal Gedanken machen wie man am Abend vorzugehen hat.