Summenwert der Binominalreihe von f(x)=\sqrt{1-x^{2}} für rationale Zahlen

Question

Aufgabe:

Summenwert der Binominalreihe von \( f(x)=\sqrt{1-x^{2}} \) für rationale Zahlen bestimmen.

Problem/Ansatz:

Ich möchte gern wissen, ob man den Summenwert der Binominalreihe von \( f(x)=\sqrt{1-x^{2}} \) direkt als rationale Zahl, also als Bruch, berechnen kann.

Also, wenn ich beispielsweise in die Binominalreihe  \( x=\frac{3}{5} \) einsetze,sollte als Ergebnis \( f(x)=\frac{4}{5} \) herauskommen.

Ich habe die Binomimalreihe wie folgt erstellt:

\( f(x)=\sqrt{1-x^{2}}=(1-x^{2})^{\frac{1}{2}}=\sum\limits_{k=0}^{\infty}\dbinom{\frac{1}{2}}{k}(-1)^{k}(x^{2k}) \)

ergibt die folgenden ersten Summanden

\( \sum\limits_{k=0}^{\infty}\dbinom{\frac{1}{2}}{k}(-1)^{k}(x^{2k})=1-\frac{1}{2}x^{2}-\frac{1}{8}x^{4}-\frac{1}{16}x^{6}-\frac{5}{128}x^{8}-\frac{7}{256}x^{10}-.... \)

Wie komme ich aber damit auf das gewünschte Ergebnis \( f(\frac{3}{5})=\dfrac{4}{5} \)  ??

Kann man eventuell Terme vereinfachen durch Ausklammern und Kürzen beim Binominalkoeffizienten? Oder lässt sich in geeigneter Weise aus der Summe ein Grenzwert für ein festen Wert x berechnen? Gibt es dafür bekannte Methoden?

"Wolfram Alpha" berechnet wahlweise:

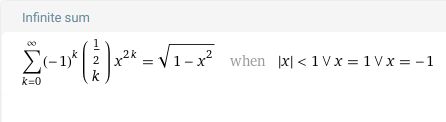
oder für \( x=\frac{3}{5} \)

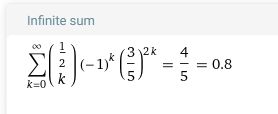
oder wenn ich für \( x=\frac{p}{q} \) eine rationale Zahl einsetze

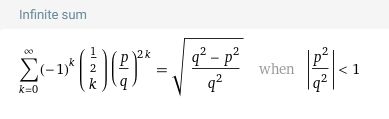
Wie machen die das bei "Wolfram Alpha" ?

Haben die einen bestimmten Algorithmus oder schauen die nur in eine Datenbank nach bekannten Funktionen?

Ich fand DIESEN Artikel sehr interessant und wollte mal probieren, ob man die Berechnungen verkürzen kann:

https://www.mathelounge.de/406129/nimmt-konvergente-unendlich-tatsachlich-nahert-beliebig

Comments

WA kennt auf jeden Fall Reihendarstellungen dieser Form und wird sich diesen Zusammenhang aus einer Datenbank ziehen. Die gegebene Funktion ist ja doch eher elementar und taucht auch hin und wieder auf.

Die Vereinfachung machen sie dann vermutlich mit der Wurzel Darstellung.

Ich meine für ein CAS ist es kein Problem

Sqrt(1-9/25)=4/5

Oder

sqrt(1-p²/q²) = sqrt((q²-p²)/q²)

auszuspucken. Aber wie es intern genau abläuft wird dir nur ein Entwickler von WolframAlpha beantworten können.

Answer 1

Ich verstehe nicht ganz warum du einen Funktionsterm in eine unendliche Reihe umformst um damit dann einen Funktionswert zu bestimmen.

Man macht es eher umgekehrt das man eine Unendliche Reihe versucht in einen expliziten Term umzuformen um damit dann Funktionswerte zu berechnen

f(3/5) = √(1 - (3/5)^2) = √(1 - 9/25) = √(25/25 - 9/25) = √(16/25) = 4/5

So rum ist das doch viel einfacher und entspannter.

Comments

Das Ziel war für mich wirklich, aus der Binominalreihe einen expliziten Ausdruck für die Berechnung des Wurzelausdrucks zu finden, was aber wahrscheinlich so nicht funktioniert.

Es ensteht keine "klassische" geometrische Reihe. Auch der Weg über gliedweises Differenzieren ergibt immer wieder nur eine Potenzreihe mit neuen Koeffizienten.

Das Differenzieren des eigentlichen Summenausdrucks scheitert bei mir daran, dass ich (noch) nicht weiss, wie man den Binominalkoeffizienten ableiten kann. Allerdings führt das wahrscheinlich auch wieder zu der o.g. Potenzreihe.

Ein interessantes Problem für mich - aber eigentlich völlig unwichtig :-)