Gesucht ist der wert der Obersumme O4 und U4

Question

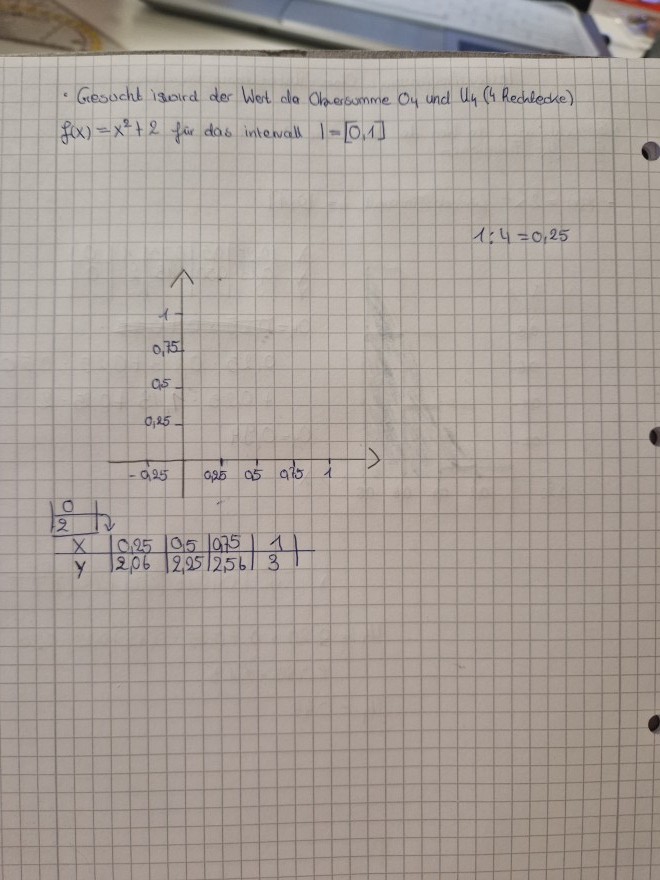
Aufgabe: Gesucht wird der wert der Obersumme 04 und U4 (4 Rechtecke )

F(x)=x²+2 für das intervall | = [0, 1]

Text erkannt:

- Gesucht isaird der Wot da Obersumme \( \mathrm{O}_{4} \) und \( \mathrm{U}_{4} \) (4 Rechtecke) \( f(x)=x^{2}+2 \) für das intervall \( 1=[0,1] \)
\( 1: 4=0,25 \)

Problem/Ansatz:

Ich glaub hier hab ich was falsch gemacht denn mein intervall geht ja nur von 0 bis 1 und meine schrittlänge hier ist hakt eben 0.25 0.5 0.75 und 1 aberrr das was ich rausbekommen geht weit über 1. Ich weiß nicht wie ich das einzeichnen soll oder wo wie was falsch ist…

(Also ich weiß schon wie man die obersumme und untersumme rauskriegen im allgemeinen aber hier bei dem hat verwirrt mich das voll)

P.s ich benutze den Casio Taschenrechner

Answer 1

aberrr das was ich rausbekommen geht weit über 1.

Das muss ja auch sein. Du sollst nicht die Fläche unter x², sondern die Fläche unter dem Graphen von x²+2 annähern. Da hast du allein mit der Teilfläche unter der Geraden y=2 (blau) einen Inhalt von 2 Flächeneinheiten...

Da kommt noch oben was drauf.

Comments

Das verwirrt mich grad einbisschen... also ist es egal wie hoch ich die y Achse hoch zeichne aber mich dafür bei der x Achse an die Beschreibung halte? Aber irgendwie ergibt sich das für mich nicht. Denn die Länge geht ja von 0 bis 1

---

Ich habe gerade eine Abbildung und meinen Kommentartext ergänzt.

---

Oh vielen dank!! Also stimmt dass das ich die y Achse "beliebig" hoch zeichnen kann aber die x Achse den Beschreibungen entsprechen muss?

---

"Wie hoch" du die y-Achse zeichnest ist doch völlig Wurst.

Wenn du allerdings die Funktion, um die es geht, tatsächlich sehen willst, musst du den y-Bereich so weit setzen, dass der Graph im betrachteten Intervall zu sehen ist.

Answer 2

Benutze doch Geogebra, um es dir zu visualisieren und ein Kontrollergebnis zu haben.

Anfangen wurde man mit einer Wertetabelle im Intervall [0; 1] mit der Schrittweite 0.25.

Deine Wertetabelle wäre schon richtig, wenn auch arg gerundet. Schreibe lieber Brüche auf, wenn du Dezimalzahlen nicht so magst.

U4 = 0.25·(2 + 2.0625 + 2.25 + 2.5625) = 2.21875

O4 = 0.25·(2.0625 + 2.25 + 2.5625 + 3) = 2.46875