Kopfrechnung wie rechne ich das ?!

Question

Aufgabe: die Summe zweier zahlen ist 17. Ihre Differenz ist 11. Geben Sie die beiden zahlen an.

…

Problem/Ansatz: ich habe keine ahnung wie ich das rechnen soll , ich schreibe nächste woche Prüfungen und hab keine ahnung

HILFEEE

Answer 1

Hallo,

du kannst die Aufgabe auch als Gleichungssystem formulieren.

1. Zahl = x     2. Zahl = y

Die Summe zweier Zahlen ist 17: x + y = 17

Die Differenz zweier Zahlen ist 11: x - y = 11

Löse das Gleichungssystem mit einem Verfahren deiner Wahl.

[spoiler]

Additionsverfahren:

\(x+y=17\\ \underline{x-y=11}\\ 2x\quad =28\\ x = 14\quad \Rightarrow y = 3\)

[/spoiler]

Gruß, Silvia

Comments

Na ja, Kopfrechnen ist das aber für Otto-Normal-Schüler nicht mehr. :-)

---

Deswegen habe ich "auch" geschrieben. ;-)

Answer 2

Probieren:

16 - 1 = 15

15 - 2 = 13

14 - 3 = 11, hurra!

Answer 3

x+y= 17

x-y= 11

addieren:

2x = 28

x= 14

-> 14-y =11

y= 3

Answer 4

Hallo,

Stelle für sowas KEINE Gleichungen auf, sondern stelle Dir die Zahlen wie lange Stöcke vor. Umso länger desto größer die Zahl.

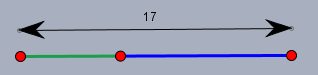
Wenn man beide Stöcke an einander legt, so sind die 17 lang (die Summe).

... und wenn man von dem längeren 11 abschneidet (also die Differenz) ...

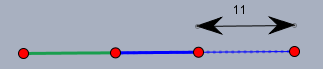
dann muss das verbleibende blaue Stück doch genauso lang sein, wie der grüne Stock. Also 17-11=6 und die Hälfte davon ist 3 ... das ist die Länge des kürzeren Stocks, bzw. die kleinere Zahl.

So kann man es auch im Kopf ausrechnen - oder?

Gruß Werner

Comments

So kann man es auch im Kopf ausrechnen - oder?

Wenn man sich das ohne Skizze vorstellen kann, dann ja.

Ob das jeder kann?

---

Wenn man sich das ohne Skizze vorstellen kann, dann ja.

Hier reicht ja 1-dimensionales Denken völlig aus. Nur 0-dimensionale Denker werden damit ein Problem haben.

Answer 5

Addiere beide: 17+11=28

Dividiere durch 2: 28/2=14

14+3=17   ;   14-3=11

:-)

Comments

Danke! Das hat mir sehr geholfen