Aufgabe:
Problem:
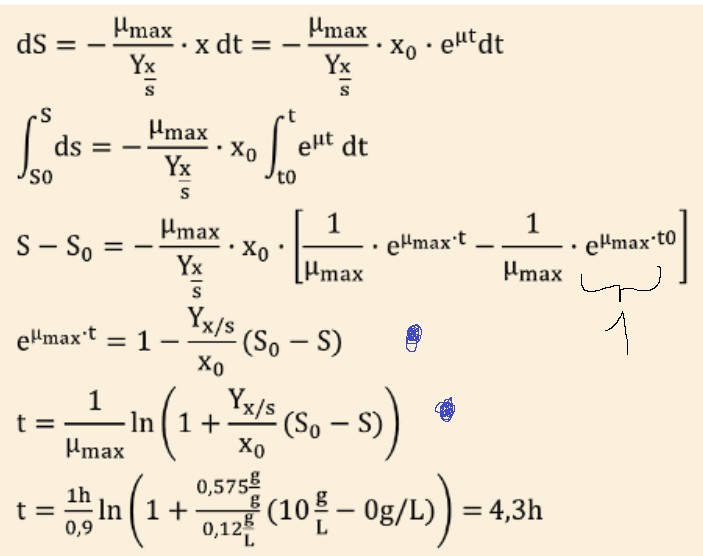
Wie kommt man von der vierten Zeile zur fünften Zeile. Ich verstehe dass man den Ln benutzt um e^ümax*t aufzulösen, aber woher kommt der Vorzeichenwechsel von 1- (yxs/X0) zu 1 + (yxs/X0). Das sollen die Lösungen sein laut Aufgabe, aber ich bin mir nicht sicher ob es zu 100% stimmt.
Text erkannt:
\( \begin{array}{l}\mathrm{t}=\frac{1}{\mu_{\max }} \ln \left(1+\frac{\mathrm{Y}_{\mathrm{x} / \mathrm{s}}}{\mathrm{x}_{0}}\left(\mathrm{~S}_{0}-\mathrm{S}\right)\right) \\ \mathrm{t}=\frac{1 \mathrm{~h}}{0,9} \ln \left(1+\frac{0,575 \frac{\mathrm{g}}{\mathrm{g}}}{0,12 \frac{\mathrm{g}}{\mathrm{L}}}\left(10 \frac{\mathrm{g}}{\mathrm{L}}-0 \mathrm{~g} / \mathrm{L}\right)\right)=4,3 \mathrm{~h} \\\end{array} \)
Text erkannt:
\( \begin{array}{l}d S=-\frac{\mu_{\max }}{Y_{\bar{s}}} \cdot x d t=-\frac{\mu_{\max }}{Y_{\bar{s}}} \cdot x_{0} \cdot e^{\mu t} d t \\ \int \limits_{S 0}^{S} d s=-\frac{\mu_{\max }}{Y_{\bar{x}}^{s}} \cdot x_{0} \int \limits_{t 0}^{t} e^{\mu t} d t \\ \mathrm{~S}-\mathrm{S}_{0}=-\frac{\mu_{\max }}{\mathrm{Y}_{\overline{\mathrm{x}}}} \cdot \mathrm{x}_{0} \cdot\left[\frac{1}{\mu_{\max }} \cdot \mathrm{e}^{\mu_{\max } \cdot \mathrm{t}}-\frac{1}{\mu_{\max }} \cdot \mathrm{e}^{\mu_{\max } \cdot \mathrm{t} 0}\right] \\ \mathrm{e}^{\mu_{\max } \cdot \mathrm{t}}=1-\frac{\mathrm{Y}_{\mathrm{x} / \mathrm{s}}}{\mathrm{x}_{0}}\left(\mathrm{~S}_{0}-\mathrm{S}\right) \\ \mathrm{t}=\frac{1}{\mu_{\max }} \ln \left(1+\frac{\mathrm{Y}_{\mathrm{x} / \mathrm{s}}}{\mathrm{x}_{0}}\left(\mathrm{~S}_{0}-\mathrm{S}\right)\right) \\ \mathrm{t}=\frac{1 \mathrm{~h}}{0,9} \ln \left(1+\frac{0,575 \frac{\mathrm{g}}{\mathrm{g}}}{0,12 \frac{\mathrm{g}}{\mathrm{L}}}\left(10 \frac{\mathrm{g}}{\mathrm{L}}-0 \mathrm{~g} / \mathrm{L}\right)\right)=4,3 \mathrm{~h}
Problem/Ansatz:
