Aufgabe:
Hallo liebe Mathe Gemeinde,
es geht um einen Beweis für das O-Kalkül. 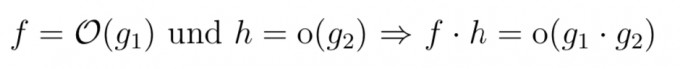
Mein Problem hierbei ist die Überführung von kleiner gleich auf streng kleiner, da die Definitionen von Groß-O und klein-o jeweils verschiedene Ordnungsrelationen haben.
Hier sind die beiden Definitionen

Kann man irgendwie den Weg gehen, dass man quasi weiß, wenn
2 <= 2 und 2 < 3, dass dann auch 2*2 < 2*3 gilt? Mir fehlt da der Beweisschritt...
Ich hoffe ihr könnt mir helfen
Vielen Dank für eure zeit.