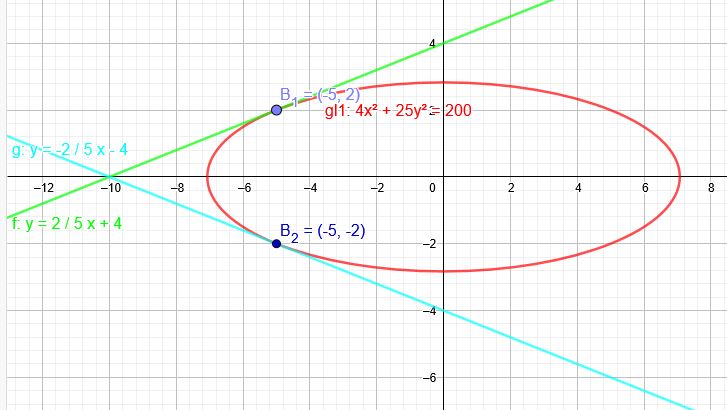
Gleichung der Tangente im Punkt \(P(-5|y)\) auf der Ellipse: \(4x^2 + 25 y^2 = 200\)
\(f(x,y)=4x^2 + 25 y^2 - 200\)
\(f'(x)=- \frac{8x}{50y}=- \frac{4x}{25y} \)
\(P(-5|2)\):
\(f'(-5)=- \frac{-20}{50} =\frac{2}{5} \)
Tangentengleichung:
\( \frac{y-2}{x+5}=\frac{2}{5} \)
\( y=\frac{2}{5}x+4 \)
2.Tangente:
\( y=-\frac{2}{5}x-4 \)