Ich komme bei Aufgabe b2 nicht weiter…Wachstumsfunktion aufstellen

Question

Im Folgenden wird die idealtypische momentane Gewichtszunahme eines Bernhardiners in
Gramm pro Tag für 0 ≤ t ≤ 217,5 durch die Funktion f mit f (t)= −0,02t2 +5,8t modelliert. Dabei gibt t die Zeit in Tagen seit der Geburt ( t = 0 ist der Zeitpunkt der Geburt, t = 1 ist das Ende des ersten Tages) und f (t ) die idealtypische momentane Gewichtszunahme in Gramm pro Tag an.
a) (1)
(2)
b)(1)
Geben Sie die idealtypische momentane Gewichtszunahme am Ende des 20. Tages an, die sich bei der Modellierung mit f ergibt.
Bestimmen Sie rechnerisch 217,5 f (t)dt und interpretieren Sie den Wert im Sach- 0
zusammenhang.
2. Die idealtypische momentane Gewichtszunahme eines Bernhardiners wird für
t≥217,5 durch die Funktion g mit g(t)=b⋅ec⋅t ,mit geeigneten b∈IR, c∈IR,
modelliert. Dabei gibt t wieder die Zeit in Tagen seit der Geburt und g (t ) die ideal- typische momentane Gewichtszunahme in Gramm pro Tag an.
Ermitteln Sie b und c so, dass gilt:
g(217,5)=f(217,5) und g'(217,5)=f'(217,5).

Problem/Ansatz:

ich komme bei b2 nicht weiter.kann mir bitte jemand helfen

Lg Sissi

Answer 1

Hallo
für 2b) brauchst du ja b1 also f(275,5) und f'(275,5) aus der vorigen Aufgabe, die einfach einsetzen in g und g' an der Stelle dann hast du 2 Gleichungen für b und c-

der Satz davor "Bestimmen Sie rechnerisch 217,5 f (t)dt" ist unklar fehlt da irgendwo ein Integral?

Bitte kontrolliere deine posts in Vorschau , dann kannst du z.B Hochzeichen etwa bei t^2 oder e^ct noch korrigieren, die ct anwählen und dann oben auf X^2 klicken z.B

Gruß lul

Answer 2

Hallo,

bilde die Ableitungen von f und g und setze in die Gleichungen 217,5 für x und die entsprechenden Funktionswerte ein.

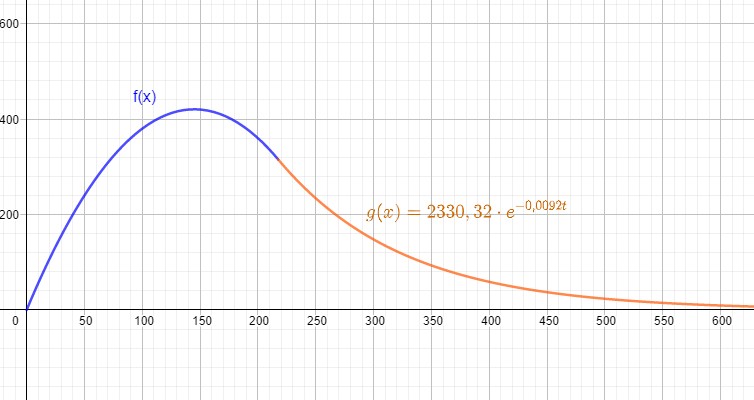
\(f(t)=-0,02t^2+5,8t\qquad f'(t)=-0,04t+5,8\\ g(t)=b\cdot e^{ct}\qquad g'(t)=c\cdot b\cdot e^{ct}\\ f(217,5)=315,375\\ f'(217,5)=-2,9\)\\

\(315,375=b\cdot e^{217,5c}\\ -2,9=c\cdot b\cdot e^{217,5c}\)

1. Gleichung : 2. Gleichung ergibt

\(-108,75=\frac{1}{c}\Rightarrow c=-\frac{4}{435}\)

Jetzt nur noch b bestimmen.

Gruß, Silvia