Hallo,
der Querschnitt der Halle hat offenbar die Form einer nach unten geöffneten Parabel.
Lege den höchsten Punkt auf die y-Achse. Daraus ergibt sich die Gleichung
\(f(x)=ax^2+10\)
Um a zu bestimmen, setzt du die Koordinaten von einer Nullstelle ein:
\(0=a\cdot 20^2+10\\ -\frac{1}{40}=a\)
Das ergibt die Gleichung \(f(x)=-\frac{1}{40}x^2+10\)
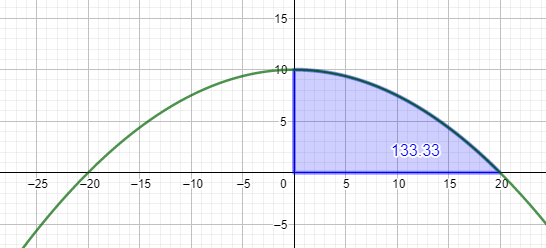
Berechne nun das \(\int \limits_{0}^{20}f(x)\;dx \) und verdopple dein Ergebnis.
Gruß, Silvia