Kosinussatz mit anderem Winkel

Question

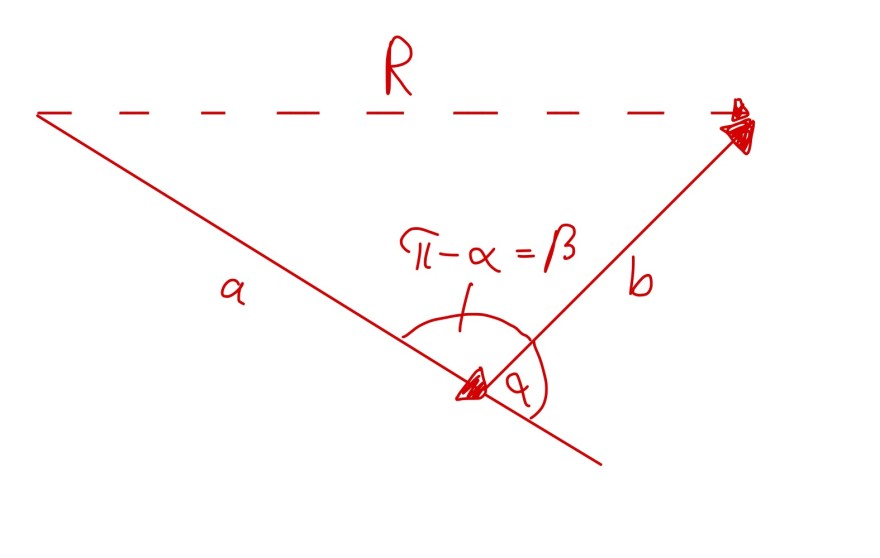
Hallo, ich habe Folgendes Problem bei einem Kräftedreieck.

Der Cosinussatz für die Resultierende R lautet ja R²=a²+b²-2ab•cos(π-α). Wobei π-α einfach der Winkel β gegenüber von R ist. Nun wird bei der Lösung ganz selbstverständlich die Wurzel gezogen, plötzlich wird aber unter der Wurzel aus der Endung „-2ab•cos(π-α)“ gleich +2ab•cos(α) und das erschließt sich mir einfach nichts und ich finde auch nirgends eine Website die das benutzt, geschweigedenn erklärt warum das scheinbar gehen soll.

Ich bedanke mich jetzt schonmal für Antworten, auf eine wahrscheinlich sogar recht triviale Aufgabe.

Comments

Kommentar -> Antwort

Answer 1

Hallo,

Der Winkel π (Bogenmaß)  entspricht 180°
Aus Symmetriegründen gilt immer cos(π - α) = - cos(α)

Gruß Wolfgang

Comments

Irgendwie stehe ich grad völlig aufm Schlauch, cos(pi) ist ja -1, cos(90grad) doch aber 0, das müsste doch eigentlich gleich sein, wenn pi=90 grad. Ansonsten verstehe ich, was du meinst.

---

Sorry, gemeint war oben natürlich 180° (korrigiert)   ( 4 Uhr :-) )

---

Ah ok, ja das macht natürlich dann Sinn mit der Symmetrie, ich hatte da einfach total den Denkfehler, danke!

Answer 2

Die Kosinusfunktion ist punktsymmetrisch zum Punkt \(\left(\frac{\pi}{2}|0\right)\). Deshalb ist

        \(-\cos(\pi - \alpha) = \cos\alpha\).