DGL Harmonische Oszillator, Anfangswertproblem Backward (implizit) Euler

Question

Aufgabe:

Hallo, kann mir jemand bei der Aufgabe helfen?
Ich verstehe nicht so ganz, wie man hier beim Backward Verfahren auf den letzten Schritt kommt. Was genau ist lambda?
Das erste Bild zeigt das Backward Euler verfahren ganz allgemein. Was genau ist jetzt y(t)/(1 - delta t * lambda) bzw. wie kommt man drauf

Problem/Ansatz:

Text erkannt:

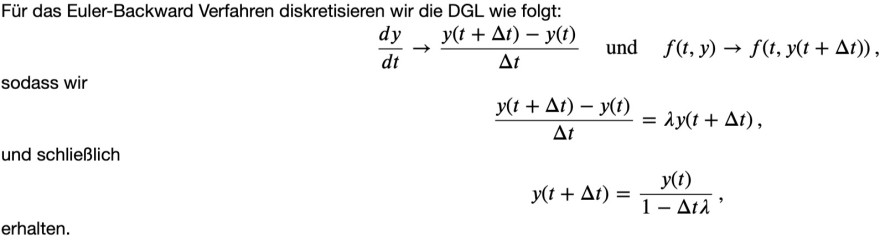
Für das Euler-Backward Verfahren diskretisieren wir die DGL wie folgt:
sodass wir
und schließlich
\( \begin{array}{c} \frac{d y}{d t} \rightarrow \frac{y(t+\Delta t)-y(t)}{\Delta t} \quad \text { und } \quad f(t, y) \rightarrow f(t, y(t+\Delta t)) \\ \frac{y(t+\Delta t)-y(t)}{\Delta t}=\lambda y(t+\Delta t) \\ y(t+\Delta t)=\frac{y(t)}{1-\Delta t \lambda} \end{array} \)
erhalten.

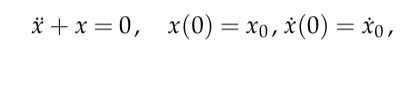
Text erkannt:

\( \ddot{x}+x=0, \quad x(0)=x_{0}, \dot{x}(0)=\dot{x}_{0} \)

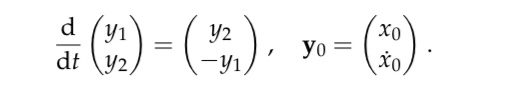
Text erkannt:

\( \frac{\mathrm{d}}{\mathrm{d} t}\left(\begin{array}{l}y_{1} \\ y_{2}\end{array}\right)=\left(\begin{array}{c}y_{2} \\ -y_{1}\end{array}\right), \quad \mathbf{y}_{0}=\left(\begin{array}{l}x_{0} \\ \dot{x}_{0}\end{array}\right) \).

Text erkannt:

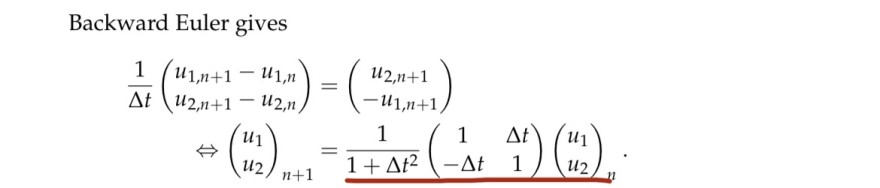
Backward Euler gives
\( \begin{aligned} \frac{1}{\Delta t}\left(\begin{array}{l} u_{1, n+1}-u_{1, n} \\ u_{2, n+1}-u_{2, n} \end{array}\right) & =\left(\begin{array}{c} u_{2, n+1} \\ -u_{1, n+1} \end{array}\right) \\ \Leftrightarrow\left(\begin{array}{l} u_{1} \\ u_{2} \end{array}\right)_{n+1} & =\frac{1}{1+\Delta t^{2}}\left(\begin{array}{cc} 1 & \Delta t \\ -\Delta t & 1 \end{array}\right)\left(\begin{array}{l} u_{1} \\ u_{2} \end{array}\right)_{n} . \end{aligned} \)

Answer 1

Es wird gestartet mit der DGL$$\frac d{dt}y = f(t,y),\; y(t_0) = y_0$$In deinem Beispiel ist mit Hinblick auf die spätere Diskretisierung des harmonischen Oszillators $$f(t,y) = \lambda y \quad (1)$$Bei einem Backward Euler Schritt erhältst du zunächst eine implizite Gleichung für \(y(t+\Delta t)\), die nach \(y(t+\Delta t)\) aufzulösen ist:$$\frac {y(t+\Delta t) - y(t)}{\Delta t} = f( t+\Delta t, y(t+\Delta t) ) \stackrel{(1)}{=} \lambda y(t+\Delta t) \quad (2)$$Diese Gleichung wird nun nach \(y(t+\Delta t)\) aufgelöst:

\((2)\Leftrightarrow y(t+\Delta t) - y(t) = \lambda \Delta t y(t+\Delta t)\)

\(\Leftrightarrow (1-\lambda \Delta t)y(t+\Delta t) = y(t)\)

\(\Leftrightarrow y(t+\Delta t) = \frac{y(t)}{1-\lambda \Delta t}\)

Das gleiche Prinzip wird dann auf den harmonischen Oszillator angewendet, nachdem die Differentialgeichung in eine System 1. Ordnung verwandelt wurde per \(y_1= x,\; y_2= \dot x\).

Beim Auflösen nach \(\begin{pmatrix} u_1 \\ u_2\end{pmatrix}_{n+1}\) erhältst du zunächst

\(\begin{pmatrix} 1 & -\Delta t \\ \Delta t & 1\end{pmatrix}\begin{pmatrix} u_1 \\ u_2\end{pmatrix}_{n+1} = \begin{pmatrix} u_1 \\ u_2\end{pmatrix}_{n}\)

Invertieren der Matrix gibt dann die von dir angegebene Formel für \(\begin{pmatrix} u_1 \\ u_2\end{pmatrix}_{n+1}\).

Comments

\( \left(\begin{array}{l}u_{2} \\ -u_{1}\end{array}\right)_{n+1} \cdot \Delta t+\left(\begin{array}{l}u_{1} \\ u_{2}\end{array}\right)_{n} \)

Wäre diese Schreibweise auch richtig? Oder habe ich was falsch gemacht?

---

\( \begin{array}{l}(2) \Leftrightarrow y(t+\Delta t)-y(t)=\lambda \Delta t y(t+\Delta t) \\ \Leftrightarrow(1-\lambda \Delta t) y(t+\Delta t)=y(t)\end{array} \)

Könntest du kurz noch erklären, wie man von der ersten Zeile auf die zweite gekommen ist. Könnte man bei der ersten Zeile nicht direkt y(t) auf die andere Seite bringen, dann hätten wir links ja schon y(t + delta t)?

---

Erstmal kurz zu deiner vorhergehenden Frage:
Den Ausdruck, den du in deinem Kommentar geschrieben hast, sehe ich nicht so auf deinen Screenshots.
Aber grundsätzlich ist die Schreibweise ok. Ich war nur verwundert, wieso aus den y plötzlich u wurden.

Zu deiner 2. Frage:
Mir ist nicht ganz klar, wie du \(y(t)\) direkt auf die andere Seite bringen willst, ohne das \(\Delta t\) im Nenner loszuwerden.

Vielleicht schreibst du hier noch in einem Kommentar, wie du das machen willst.

---

1) Also Ist der Ausdruck, den ich als Kommentar verfasst habe, der selbe wie der Ausdruck, den ich den in Screenshots rot unterstrichen habe? Also wäre das grundsätzlich die Lösung

2) Also nachdem ich Delta t vom Nenner auf die rechte Seite gebracht habe. Dann hätte ich auf der linken Seite ja y(t+Δt)−y(t) oder?

---

1) Genau. Das ist die Lösung.

2) Nochmal genau. Aber du kommst nicht drumherum, nach \(y(t+\Delta t)\) aufzulösen. Wie du das machst, ist egal, solang alle Umformungen korrekt sind. Das richtige Ergebnis kennst du ja.

---

2) sorry nochmal kurz zum Verständnis, also wenn ich jetzt hier

y(t+Δt)−y(t)=λΔty(t+Δt). y(t) auf die andere Seite bringe, dann hätte ich ja

y(t+Δt) = λΔty(t+Δt)+y(t) und das wäre dann das gleiche wie  y(t+Δt)= y(t)/(1−λΔt)

---

Klar. Alles richtig. Ich habe vorsichtshalber noch einen Rechenschritt eingebaut.
Wenn du das Ergebnis direkt siehst - perfekt. :-)

---

Super vielen vielen Dank, hast mir sehr geholfen.

---

Letzte Nachfrage versprochen:

y(t+Δt)−y(t)=λΔty(t+Δt)

\(\Leftrightarrow (1-\lambda \Delta t)y(t+\Delta t) = y(t)\)

Ich verstehe hier leider noch nicht so ganz, wie du auf die zweite Zeile gekommen bist. Also klar, hast y(t) auf die rechte Seite gebracht und das andere auf die Linke, aber wie genau hast du es auf die Linke Seite gebracht, bzw. wie kommst du auf

\( (1-\lambda \Delta t) y(t+\Delta t) \)

Was genau hast du hier gerechnet

---

Ich habe \(y(t+\Delta t)\) als gemeinsamen Faktor auf der linken Seite der Gleichung ausgeklammert:

$$y(t+\Delta t) - \lambda \Delta t y(t+\Delta t) = (1 - \lambda \Delta t )y(t+\Delta t)$$

---

Ahh jetzt sehe ich es, danke!