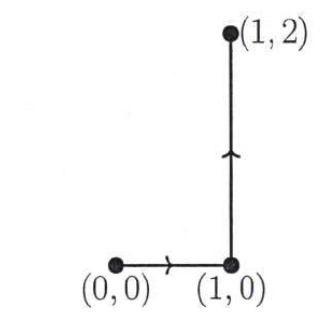
Aufgabe:
Ich habe eine Kurve gegeben welche die Punkte wie in der Abbildung oben miteinander verbindet. Ausgehend hiervon, soll ich eine stückweise glatte Parametrisierung der Kurve ɣ finden und die Bogenlänge L(ɣ) berechnen.
Problem/Ansatz:
Ich habe Schwierigkeiten damit genau zu verstehen was hier zu tun ist. Ich hätte die Aufgabe in zwei Teilen unterteilt: Einmal die Parametrisierung zwischen (0,0) und (1,0), und dann noch zwischen (1,0) und (1,2). Insgesamt sieht die Parametrisierung dann so aus:
ɣ(t) = (t,0) + (1,2t), t ∈ [0,1]
da die Strecke zwischen (0,0) und (1,0) sich wie folgt parametrisieren lässt: (0,0) + t*((1,0)-(0,0)) = (t,0) und
die Strecke zwischen (1,0) und (1,2) lässt sich wie folgt parametrisieren: (1,0) + t*((1,2)-(1,0)) = (1,2t) und
Hier auch direkt die erste Frage, ist die Parametrisierung richtig, wenn nein, wie müsste ich hier sonst vorgehen?
Die Länge der Kurve wäre entsprechend nach Definition \( \int\limits_{0}^{1} \) ||ɣ'(t)|| dt = \( \int\limits_{0}^{1} \) \( \sqrt{(1-0)^{2} + (0-2)^{2}} \) dt = [\( \sqrt{5} \)t ]01 = \( \sqrt{5} \).
Ich schätze mal, ich wüsste gern wie man hier vorgehen muss, bzw., ob mein Ansatz vielleicht sogar schon passt?
Vielen Dank!