Berechnen sie die Fläche zwischen Gf und der Abzissenachse.

Question

Aufgabe:

Gegeben ist die Funktion

f(x)= (1/8x^3)-(3/4x^2)+4

a.)

Berechnen sie die Fläche zwischen Gf und der Abzissenachse.

b.)

Die Fläche wird durch die Gerade g=x‘ in zwei Teile zerlegt.

Der obere hat den Flächeninhalt A1, der untere A2.

Bestimmen sie A1.

c.)

Wie groß ist der Anteil von A1 an A in Prozent?
Problem/Ansatz:

Könnte es mir bitte jemand erklären?

Danke

Comments

Mach eine Skizze davon.

Answer 1

Willkommen in der Mathelounge!

\(f(x)=\frac{1}{8}x^3-\frac{3}{4}x^2+4\)

Bestimme die Nullstellen der Funktion und berechne anschließend das Integral zwischen ihnen.

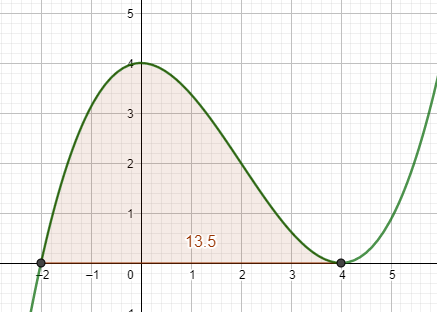
b) Berechne die Schnittpunkte von f und g, indem du die Funktionsterme gleichsetzt:

\(\frac{1}{8}x^3-\frac{3}{4}x^2+4=x\)

und nach x auflöst.

Berechne dann das \(\int \limits_{-2}^{0}f(x)\) (grün) und das \(\int \limits_{0}^{2}f(x)-g(x)\) (blau).

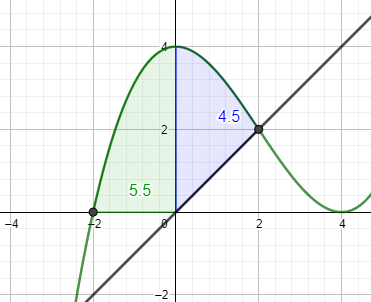
Addiere beide Flächeninhalte zu A1.

Der Anteil an der Gesamtfläche beträgt 10 : 13;5 = 0,74 = 74 %

Melde dich, falls du dazu noch Fragen hast.

Gruß, Silvia

Comments

Kannst du a.) nochmal erklären, bitte :)

---

Berechnen sie die Fläche zwischen Gf und der Abzissenachse.

Du sollst die Fläche zwischen dem Graphen von f (grün) und der x-Achse berechnen.

Die Punkte, die diese Fläche begrenzen, sind die Nullstellen der Funktion.

Löse also die Gleichung \(\frac{1}{8}x^3-\frac{3}{4}x^2+4=0\) nach x auf.

Der Flächeninhalt wird berechnet mit

\( \begin{aligned} & \int \limits_{-2}^{4}\left(\frac{1}{8} x^{3}-\frac{3}{4} x^{2}+4\right) d x \\ = & {\left[\frac{1}{32} x^{4}-\frac{1}{4} x^{3}+4 x\right]_{-2}^{4} }\end{aligned} \)

\( =\frac{1}{32} \cdot 4^{4}-\frac{1}{4} \cdot 4^{3}+4 \cdot 4-\left(\frac{1}{32} \cdot(-2)^{4}-\frac{1}{4}(-2)^{3}+4 \cdot(-2)\right.\\=8-(-5,5)=13,5 \)

---

Dankeschön :)

Was ich noch nicht verstehe, ist die Aufgabe b.)

Das mit den Integralen. Ich habe noch nie mit Integralen gearbeitet.

Könntest du mir es nochmal erklären, wenn es dir nichts ausmacht.

Danke

---

Die Gerade g = x teilt den Flächinhalt aus a) in A1 (grün) und A2 (blau).

Die grüne Fläche musst du unterteilen.

orange ist das \(\int \limits_{-2}^{0}f(x)\), also die Fläche zwischen f und der x-Achse im Intervall von -2 bis 0.

grün ist das Integral zwischen f und g im Intervall von 0 bis 2 (= Schnittpunkt von f und g).