Winkelfunktionen für beliebige Winkel

Question

Aufgabe:

Text erkannt:

\( \sin (\alpha)=\frac{\text { Gegenkathete von } \alpha}{\text { Hypotenuse }} \quad \cos (\alpha)=\frac{\text { Ankathete von } \alpha}{\text { Hypotenuse }} \quad \tan (\alpha)=\frac{\text { Gegenkathete von } \alpha}{\text { Ankathete von } \alpha} \)
- Umrechnung vom Gradmaß ins Bogenmaß:
\( x=\frac{\pi \cdot \alpha}{180^{\circ}} \text { rad } \quad \text { ( } \alpha \text { in Grad, } x \text { in Radiant) } \)
5.1 Eine Tür ist \( 80 \mathrm{~cm} \) breit, sie wird um die angegebenen Winkel geöffnet. Berechne jeweils die Koordinaten des Punkts \( P \).
1) \( 30^{\circ} \)
\( \begin{array}{ll}\text { 2) } 70^{\circ} & \text { 3) } 90^{\circ}\end{array} \)
4) \( 110^{\circ} \)
5) \( 150^{\circ} \)
Vergleiche die Werte für die Winkel \( 30^{\circ} \) und \( 150^{\circ} \) sowie für \( 70^{\circ} \) und \( 110^{\circ} \). Was fällt dir dabei auf?

Problem/Ansatz:

Kann mir jemand dieser Aufgabe erklären? Danke

Answer 1

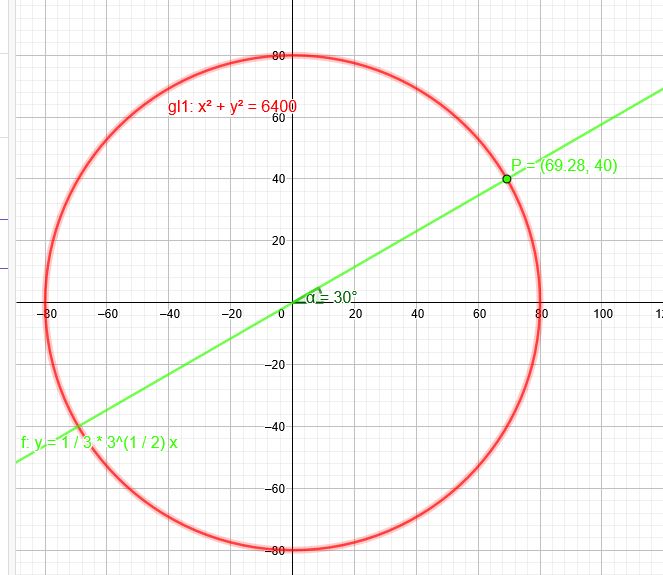
5.1 Eine Tür ist \( 80 \mathrm{~cm} \) breit, sie wird um die angegebenen Winkel geöffnet. Berechne jeweils die Koordinaten des Punkts \( P \).

Kreis um \(M(0|0)\)  mit \(r=80\) :    \(x^2+y^2=6400\)

\(y=tan(30°)*x \)  →  \(y=\frac{1}{3}*\sqrt{3}*x \)

Schnitt mit Kreis:

\(x^2+(\frac{1}{3}*\sqrt{3}*x)^2=6400\)

\(x^2+\frac{1}{3}x^2=6400\)

\(\frac{4}{3}*x^2=6400\)    →  \(x^2=3*1600\)

→  \(x_1=\sqrt{3}*40\)  →

 \(y_1=\frac{1}{3}*\sqrt{3}*\sqrt{3}*40 =40\)

Answer 2

1. 80·[cos30°|sin30°] 2. 80·[cos70°|sin70°] 3. ·[cos90°|sin90°] 4. ·[cos110°|sin110°], 5. 80·[cos150°|sin150°].

Vergleiche die Werte für die Winkel \( 30^{\circ} \) und \( 150^{\circ} \)

sowie für \( 70^{\circ} \) und \( 110^{\circ} \). Was fällt dir dabei auf?

Punkte spiegelsymmetrisch zur y-Achse