Man betrachte folgende Abbildung:
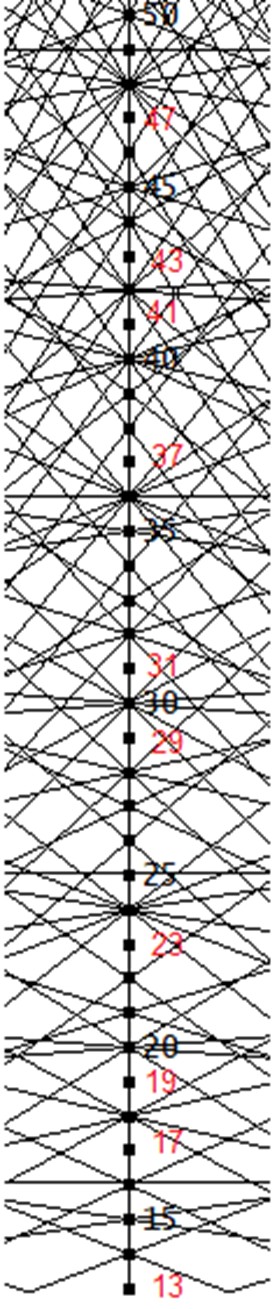
Die Abbildung zeigt einen Ausschnitt aus einer Schaar von Geraden, von denen jede einzelne durch die beiden Punkte (a|a2) und (-b|b2) für je ein gegebenes natürliches Zahlenpaar (a|b) mit a≠1 und b≠1 festgelegt ist. Die Punkte mit natürlichen Werten sind auf der y-Achse eingezeichnet und zum Teil auch beschriftet. Durch die meisten eingezeichneten Punkte gehen Geraden, nicht jedoch durch die rot bezeichneten Punkte, die man unschwer als Primzahlen identifiziert. Wenn man will, kann man im Anlegen dieser Graphik ein Primzahlensieb sehen, wobei genau die Primzahlen nicht von einer Geraden der Schar herausgestrichen werden.
Warum ist das so? Die Gleichungen der Geraden der Schaar werden in Zwei-Punkte Form so dargestellt:
(a2-b2)/(a+b)=(y-b2)/(x+b).
Durch Umformung gewinnt man daraus
y=(a-b)∙x+a∙b.
Geraden durch die beiden Punkte (a|a2) und (-b|b2) haben folglich alle natürlichen Produkte a∙b als y-Achsenabschnitt mit a≠1 und b≠1. Da bleiben zwangsläufig nur die Primzahlen übrig. Der kleine Fehler dieses Siebes, die 1 als Primzahl übrig zu lassen, kann leicht korrigiert werden. Übrigens: Die Anzahl der Geraden durch den Punkt (0|n) ist gleich der Anzahl der echten Teiler von n.