A(-6/-7) ; B(-1/-7)=1 Gleichung Berechnen

Question

A(-6/-7) ; B(-1/-7) = 1


Ich weiß nicht mal, was ich hier vor mir habe. Kann jemand einen Hinweis geben was das ist und wie es berechnet wird?

Comments

Hi,

was hat denn das =1 zu bedeuten?

Du sollst doch sicher eine Geradengleichung aus den beiden Punkten basteln?

---

Das =1 habe ich ergänzt. Sorry, mein Fehler.

Kann es sein, dass diese Gleichung 1 ergibt?

Answer 1

Hi,

ok, wenn wir nur diese beide Punkte haben und eine Geradengleichung aufstellen sollen, so gehe so vor:

 

Wissen, dass die Geradengleichung die Form y = mx+b hat. Unbekannt sind also m und b.

Einsetzen der Punkte um ein Gleichungssystem aufzustellen:

-7 = -6*m+b

-7 = -1*m+b

Beide nach b auflösen und gleichsetzen:

-7+6m = -7+m  |+7-m

5m = 0

 

Damit in die erste Gleichung:

b = -7

 

Folglich lautet die Geradengleichung y = -7.

 

Mit "geübten" Auge hätte man erkannt, dass die y-Werte bei beiden Punkten gleich sind und deshalb die Gerade eine Konstante sein muss. Dann hätte man sich die Rechnung sparen können ;).

 

Grüße

Answer 2

 

wenn eine Gerade durch A(-6|-7) und B(-1|-7) geht, kannst Du zur Erstellung der Geradengleichung folgendermaßen vorgehen:

 

Geradengleichung allgemein: y = mx + b {m ist der Anstieg, b der y-Achsenabschnitt}

Um den Anstieg zu berechnen, dividierst Du die "y-Differenz" durch die "x-Differenz":

(-7 - (-7)) / (-1 - (-6)) = 0/5 = 0

Also lautet unsere Geradengleichung jetzt

y = 0 * x + b

Wir setzen, um b herauszufinden, einen der beiden Punkte in diese Gleichung ein, zum Beispiel A:

-7 = 0 * (-6) + b

b = - 7

Damit lautet die Geradengleichung

y = 0 * x - 7 = - 7

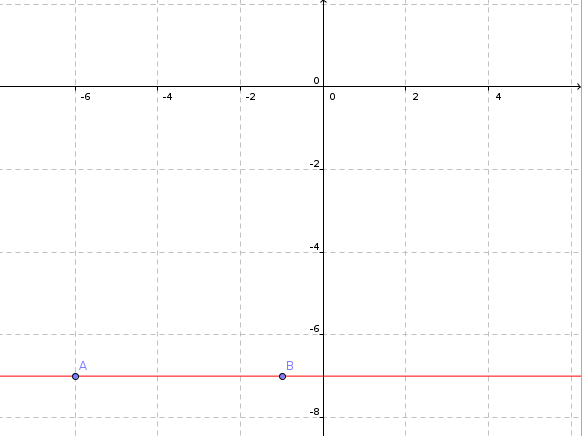
Wie man sieht, liegen die Punkte A(-6|-7) und B(-1|-7) auf der Geraden.

f(1) = -7

 

Hoffe, dass dies ein wenig hilft :-)

 

Besten Gruß

Comments

Sorry aber ich muss nochmal grundsätzlich fragen: ist das wirklich was mit Geradengleichung? Ich hatte eine hier als Beispiel geschrieben aber ich hab' noch mehr.

 

A(-6/-8) ; B(-6/-10) ; C(-3,5/-10) ; D(-3.5/-8) ; E(-1/-8) ; F(-1/-10)
A(-6/-7) ; B(-1/-7)
A(-6/-6) ; B(-6/-5) ; C(-3.5/-5) ; D(-3.5/-6) ; C(-3,5/-5) ; E(-1/-5) ; F(-1/-6)
A(-6/-4) ; B(-1/-4)
A(-6/-3) ; B(-6/-1) ; C(-3,5/-1) ; D(-3,5/-3) ; E(-1/-3) ; F(-1/-1) ; C(-3.5/-1) ; D(-3,5/-3) ; A(-6/-3)
A(-6/3) ; B(-6/1) ; C(-3,5/1) ; D(-3.5/3) ; E(-1/3) ; F(-1/1)
A(-6/4) ; B(-6/6) ; C(-3,5/6) ; D(-3,5/4) ; E(-1/4) ; F(-1/6) ; C(-3.5/6) ; D(-3.5/4) ; A(-6/4)

 

Das soll ein kleines Rätsel sein, um Zahlen zu erhalten. Nur ich kann damit nichts anfangen. :-(

http://www.geocaching.com/geocache/GC2QFQQ_die-diebeskammer?guid=2df2b528-8983-405b-96af-d8badfec6948

---

Oh sorry,

ich bitte Dich, diese komplexe Geschichte als eine neue Aufgabe zu posten, weil ich jetzt wirklich überfragt bin :-)

---

Das wäre unverschämt dem Owner der Geocachers gegenüber.

Er hat sich solch Mühe gemacht den einen oder anderen Rätseln zu lassen.

Es hat keinen Sinn die Lösung im Internet zu verbreiten und die Arbeit des Cachers mit Füßen zu treten.

Wenn es Probleme mit der Aufgabe gibt, dann bitte beim Cacher melden! Er steht sicher mit ein paar Tipps zu Verfügung.

---

Wie ich geschrieben habe, wollte ich nicht die Lösung, sondern nur grundsätzlich wissen, was das ist.