Hallo,
mache Dir eine Skizze (das sollte man immer tuen!)
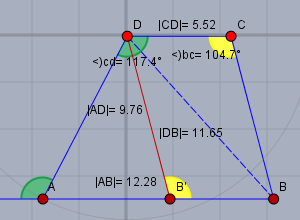
Zeichne zusätzlich eine Parallele zu einer der beiden Schenkel ein. Oben habe ich die Parallele (rot) zu \(BC\) durch \(D\) eingetragen. Die Parallele schneidet die Grundseite in \(B'\)
Die grün und gelb markierten Winkel sind gegeben. Nun kann man die Strecke \(|AB'|\) berechnet indem man den Sinussatz im Dreieck \(\triangle AB'D\) anwendet. \(|AB|\) ist dann die Summe aus \(|AB'|\) und \(|B'B|=|CD|\).
Anschließend kann man dann mit dem Cosinussatz im Dreick \(ABD\) die Länge der Diagonale \(|BD|\) berechnen.
Falls Du dazu noch Frage hast, so melde Dich bitte.
Gruß Werner