Konstruiere Strecke mit Zirkel und Lineal

Question

Geg.: Strecke der Länge 1

Konstruiert werden muss nun eine Strecke der Länge √\( \frac{1}{3} \) und zwar nur mit Zirkel und Lineal. Ich bin leicht überfordert und würde mich über jeden Ansatz freuen…

Answer 1

\( \sqrt{\frac{1}{3}}=\frac{1}{3}*\sqrt{3} \)

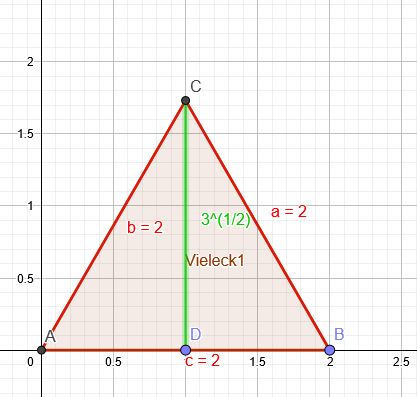
Konstruiere ein gleichseitiges Dreieck mit der Seitenlänge 2cm. Die Höhen in diesem Dreieck haben die Länge \( \sqrt{3}cm \) Jetzt musst du noch diese Höhe in 3 Teile teilen.

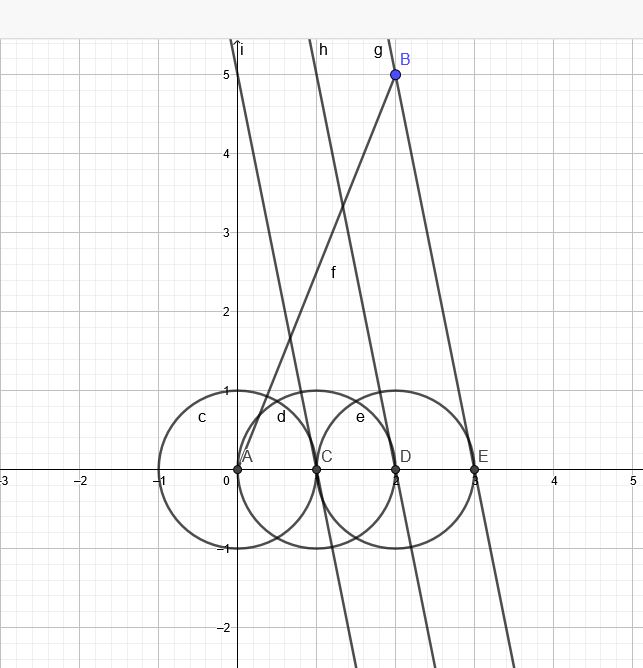
Teilung der Strecke AB in 3 Teile:

Comments

Und wenn man die Strecke anhand des Höhensatzes konstruiert? Dann muss es doch ein rechtwinkliges Dreieck sein oder?

---

Und wenn man die Strecke anhand des Höhensatzes konstruiert? Dann muss es doch ein rechtwinkliges Dreieck sein oder?

In dem Fall muss das Dreieck rechtwinklig sein. Aber leider weiß ich den Weg über den Höhensatz nicht.

---

\(tan(60°)= \sqrt{3} \) Das kann auch konstruiert werden.

Answer 2

Hallo

1/√3=√3/3 Die Höhe im gleichseitigen Dreieck mit Seite s  ist 1/2√3 *s , die kannst du leicht konstruieren undoder benutze Höhensatz h^2=p*q mit p=1,q=3 Thaleskreis und Höhe .

Gruß lul