Aufgabe:
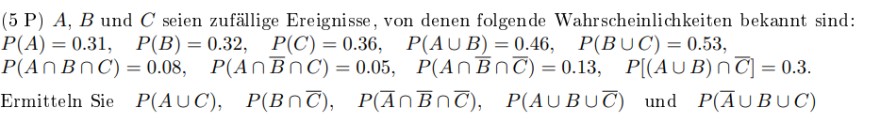
Text erkannt:
(5 P) \( A, B \) und \( C \) seien zufällige Ereignisse, von denen folgende Wahrscheinlichkeiten bekannt sind:
\( \begin{array}{l} P(A)=0.31, \quad P(B)=0.32, \quad P(C)=0.36, \quad P(A \cup B)=0.46, \quad P(B \cup C)=0.53, \\ P(A \cap B \cap C)=0.08, \quad P(A \cap \bar{B} \cap C)=0.05, \quad P(A \cap \bar{B} \cap \bar{C})=0.13, \quad P[(A \cup B) \cap \bar{C}]=0.3 . \end{array} \)
Ermitteln Sie \( \quad P(A \cup C), \quad P(B \cap \bar{C}), \quad P(\bar{A} \cap \bar{B} \cap \bar{C}), \quad P(A \cup B \cup \bar{C}) \quad \) und \( \quad P(\bar{A} \cup B \cup C) \)
Problem/Ansatz
Ich verstehe nicht ganz, wie ich bei der ersten Potenzmenge P(A U C) vorgehen muss.. Ich hätte mit der Siebformel angefangen und sie dann versucht umzustellen, aber weiter weiß ich leider auch nicht.