bestimmen Sie die Menge aller Punkte, in denen sie stetig ist).

Question

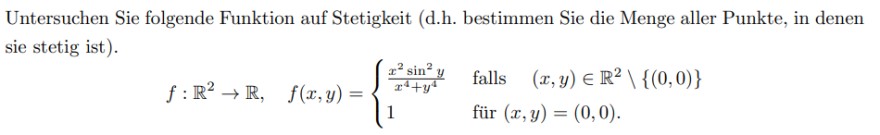
Text erkannt:

Untersuchen Sie folgende Funktion auf Stetigkeit (d.h. bestimmen Sie die Menge aller Punkte, in denen sie stetig ist).
\( f: \mathbb{R}^{2} \rightarrow \mathbb{R}, \quad f(x, y)=\left\{\begin{array}{ll} \frac{x^{2} \sin ^{2} y}{x^{4}+y^{4}} & \text { falls } \quad(x, y) \in \mathbb{R}^{2} \backslash\{(0,0)\} \\ 1 & \text { für }(x, y)=(0,0) . \end{array}\right. \)

Aufgabe:

Problem/Ansatz:Wie beweist man,dass es bei 1 nicht stetig ist?

Comments

Wie beweist man,dass es bei 1 nicht stetig ist?

Die Frage ergibt keinen Sinn. \(1\) gehört nicht zum Definitionsbereich von \(f\).

Answer 1

Man kann sich mit x=y an die Stelle (0,0) annähern. Der entstehende Grenzwert dürfte 1/2 sein.

Answer 2

Auf der Geraden \(y=x\) gilt

für \(x\neq 0\): \(\; f(x,x)=\frac{1}{2}\cdot (\frac{\sin(x)}{x})^2\rightarrow \frac{1}{2}\neq 1\)

für \(x\to 0\).