Aufgabe:
Es soll nach x aufgelöst werden. Dabei soll kein anderer Logarithmus als der natürliche log = exp^-1 verwendet werden.
Problem/Ansatz:
Ich komme nicht weiter. Kann mir jemand helfen?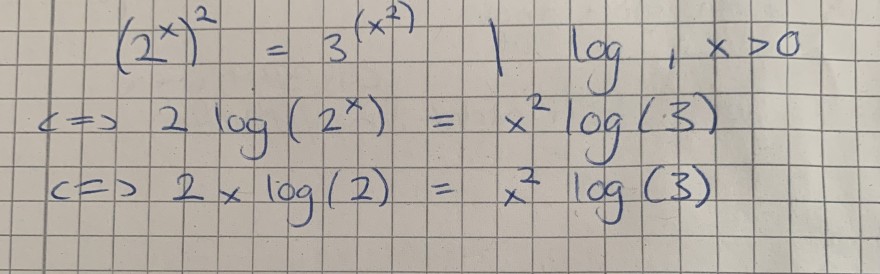
Text erkannt:
\( \begin{array}{l}\left(2^{x}\right)^{2}=3^{\left(x^{2}\right.} \quad \mid \quad \log , x>0 \\ c \Rightarrow 2 \log \left(2^{x}\right)=x^{2} \log (3) \\ c \Rightarrow 2 x \log (2)=x^{2} \log (3)\end{array} \)