Aufgabe:
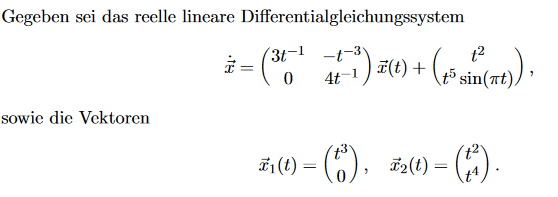
Text erkannt:
Gegeben sei das reelle lineare Differentialgleichungssystem
\( \dot{\vec{x}}=\left(\begin{array}{cc} 3 t^{-1} & -t^{-3} \\ 0 & 4 t^{-1} \end{array}\right) \vec{x}(t)+\left(\begin{array}{c} t^{2} \\ t^{5} \sin (\pi t) \end{array}\right), \)
sowie die Vektoren
\( \vec{x}_{1}(t)=\left(\begin{array}{c} t^{3} \\ 0 \end{array}\right), \quad \vec{x}_{2}(t)=\left(\begin{array}{c} t^{2} \\ t^{4} \end{array}\right) \)

Text erkannt:
ii) Geben Sie die allgemeine Lösung des (inhomogenen) DGL-Systems an.
iii) Ermitteln Sie die Lösung des Anfangswertsproblem
\( \vec{x}(1)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) . \)
Problem/Ansatz:
Könnte mir jemand bei diesen zwei Teilaufgaben behilflich sein und mir sagen wie man auf die Lösung kommt? habe es versucht aber zum entschluss gekommen das ich nicht weiterkomme :(