7000€ mit Verzinsung 4% von Bank

Question

Aufgabe:

Josef hat sich 7000€ mit 4% Verzinsung, dür die Einrichtung seiner neuen Wohnung, von der Bank geliehen. Er kann monatlich 100€ zurückzahlen.

a) Wie hoch ist die Jahresrate, die er zurückzahlen?

b) Wie lange muss sie zurückzahlen? Erstelle einen Schuldentilgungsplan.

c) Macht es sinn für Kleidung oder Urlaubsreisen einen Kredit aufzunehmen?

Problem/Ansatz:

kann mir vl bitte jemand bei dieser Aufgabe helfen? Vielen Dank!

Answer 1

Josef hat sich 7000€ mit 4% Verzinsung, dür die Einrichtung seiner neuen Wohnung, von der Bank geliehen. Er kann monatlich 100€ zurückzahlen.

a) Wie hoch ist die Jahresrate, die er zurückzahlen?

Alles Zahlungen auf den Barwert abzinsen

∑(100·(1 + 0.04·n/12), n, 0, 11) = 1222

b) Wie lange muss sie zurückzahlen? Erstelle einen Schuldentilgungsplan.

n = LN(R/(R - Bn·(q - 1))) / LN(q)
n = LN(1222/(1222 - 7000·(1.04 - 1))) / LN(1.04) = 6.635 Jahre ; Also 7 Jahre

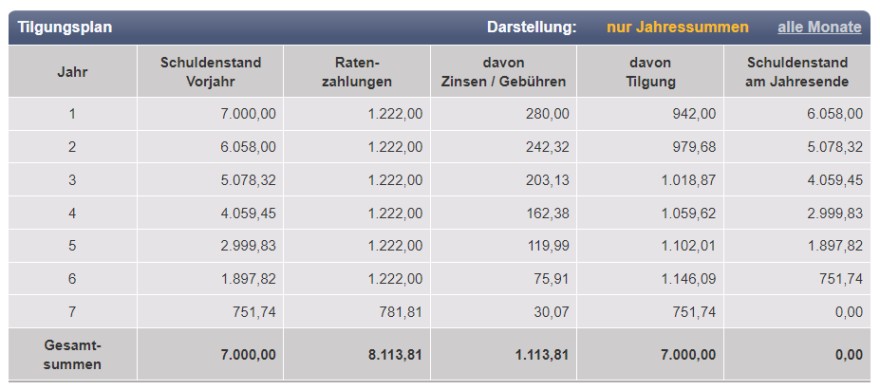
c) Macht es Sinn für Kleidung oder Urlaubsreisen einen Kredit aufzunehmen?

Meiner Meinung nach macht es meist keinen Sinn einen Kredit aufzunehmen. Außer in ganz dringenden Fällen. Ansonsten sollte man immer erst sparen und sich erst dann Dinge kaufen.

Comments

danke! wie komm ich bei der b) auf n?

---

wie komm ich bei der b)

Was meinst du? Ich habe die nötige Formel hingeschrieben als auch für unwissende die nötigen Daten in die Formel eingetragen? Was verstehst du nicht?

---

sry meine bei a) wie du auf die 1222 kommst

---

Ich zahle am Monatsende immer 100 Euro ein und zinse das auf einen gemeinsamen Endbetrag nach 12 Monaten auf.

D.h. die erste Einzahlung wird über 11 Monate verzinst und die letzte Einzahlung wird nicht mehr verzinst.

---

ah ok, bedeutet also, dass ich 11 rechnungen durchführen muss und dann die Ergebnisse einfach addieren?

---

Das kannst du machen. Es gibt natürlich auch für Unterjährige Verzinsung eine Formel

100·(12 + (0 + 11)/2·0.04) = 1222

---

danke, warum /2?

---

Das wäre die mittlere Laufzeit, mit der die 100 euro verzinst werden.

Wie gesagt, das Kürzeste sind 0 Monate und das Längste sind 11 Monate.

---

ah ok, vielen Dank

Answer 2

a) 12*100 = 1200

b) 7000*q^n = 100*(q^n-1)/(q-1)

q= 1+0,04/12, n in Monaten

Zum Rechnen: Setze q^n = z

c) 4% ist kein hoher Zins. Man muss es sich leisten können. Vorsicht Schuldenfalle!

Besser ist sparen allemal und dabei Zinsen kassieren, 1000 Euro Zinsen sind steuerfrei für jeden Deutschen.

Comments

DANKE !

wenn ich die b) berechne komme ich auf n=0, kann nicht stimmen oder

---

Wenn ich monatlich 100 Euro an die Bank zahle wäre ich sehr enttäuscht, wenn sie das nicht ordentlich verzinsen und jährlich nur 1200 Euro tilgen.

---

https://www.wolframalpha.com/input?i=+7000*q%5En+%3D+100*%28q%5En-1%29%2F%28q-1%29%2C+q%3D+1%2B0.04%2F12

n= 79,8 Monate = ca. 6 Jahre 8 Monate