Ich habe dir hier erst mal die gegebene Funktion (blau) aufgezeichnet und dazu rot y = 2 sin(2x)
2x im Argument bedeutet ja, dass die Länge einer Schwingung auf 2 pi/ 2 = pi verkürzt wird. - pi/2 im Argument macht aus dem Cosinus einen Sinus.
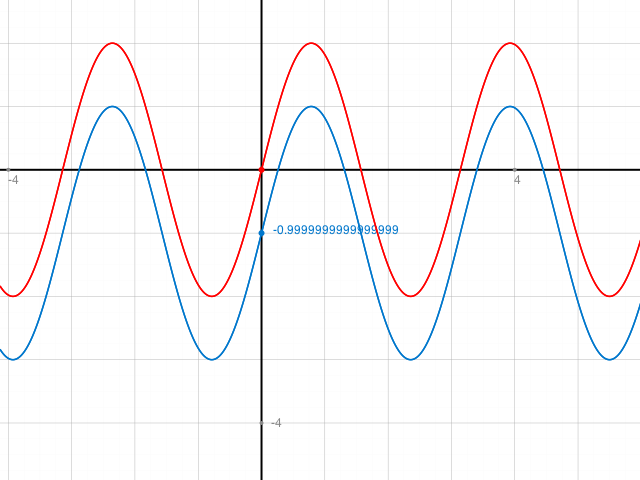
y= 2*cos(2x-pi/2)-1
Nun wollte ich gleich 0 setzen auflösen und substituieren
Dann steht da jetzt ja:
1/2 = cos(b)
b = 2x - pi/2
und invcos(1/2) ist ja 60 grad also b = pi/3 = 2x- pi/2
2x =pi/3 + pi/2 = 5 pi/6
x= 5pi/12 =1.308997 Damit hast du die zweite Nullstelle der blauen Kurve berechnet
Weil die Periodenlänge ja jetzt pi ist, bei der blauen und der roten Kurve hast du nun die Hälfte der Nullstellen der blauen Kurve.
x1 = 5pi/12 + k pi
Aus Symmetriegründen (rot und blau sind symmetrisch bezüglich pi/4 (der Vertikalen durch das erste Maximum der beiden Kurven))
x2 = pi/4 - (5pi/6 - pi/4) = pi/2 - 5pi/6 = pi/6.
Deshalb inkl. Periode: x2 = pi/6 + k pi