Konstruktion mit Zirkel und Lineal: Dreieck aus Seite, Höhe und Winkel

Question

Zul Konstruktion: konstruiere ein Dreieck aus der Seite C, der Höhe hc (senkrecht auf c) und dem der Seite c gegenüberliegendem Winkel.

Text erkannt:

\( \overline{Z Z K} \)

Answer 1

Hallo und willkommen in der Mathelounge,

Das Zauberwort heißt in diesem Fall Faßkreisbogen.

Zeichne die Strecke \(c\) mit den Endpunkten \(A\) und \(B\). Konstruiere die Mittelsenkrechte \(m\) (schwarz gestrichelt) der Strecke \(AB\). Trage den Winkel \(\gamma\) (gelb) unterhalb von \(AB\) in \(A\) an. Das Lot (lila) im Punkt \(A\) zum Schenkel von \(\gamma\) schneidet die Mittelsenkrechte \(m\) in \(U\). Zeichen den Kreis um \(U\) mit Radius \(UA\).

Die Parallele (hellblau) zu \(AB\) im Abstand \(h_c\) scheidet den Kreis in zwei Punkten \(C\) und \(C'\). \(\triangle ABC\) und \(\triangle ABC'\) sind die beiden gesuchten Dreiecke. Sie sind bis auf die Spiegelung an \(m\) identisch.

Gruß Werner

Answer 2

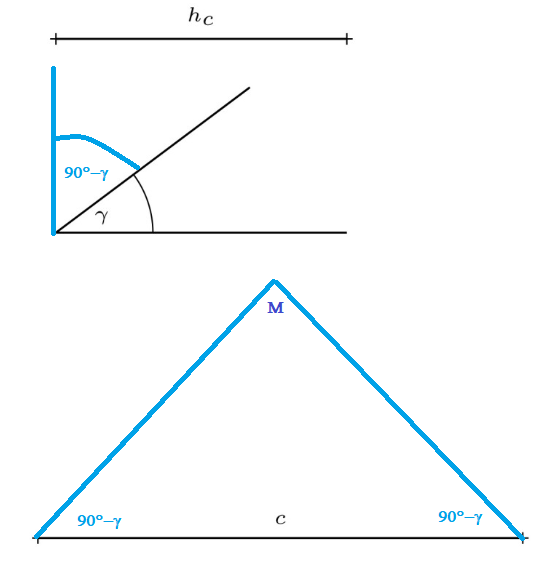
So konstruierst du den Umkreismittelpunkt M dieses Dreiecks. Der Zentriwinkel bei M hat dann die Größe 2γ.

Diese Größe muss er auch haben, weil vom Peripheriewinkel bei C die Größe γ gefordert ist.

C liegt also irgendwie auf dem Kreis um M, in dem c eine Sehne ist.

C hat außerdem von c den Abstand h_c. Alle Punkte mit dieser Eigenschaft liegen auf einer Paralle zu c im Abstand h_c.

Die Schnittpunkte des Kreises mit dieser Parallelen ergeben die zwei möglichen Lagen des Punktes C.