Welche Maße hat diese rechteckige Platte, und wie viel Prozent der ursprünglichen Plattenfläche nimmt sie ein?

Question

Aufgabe:

Von einer rechteckigen Marmorplatte ist eine Ecke abgebrochen (vgl. Abbildung). Aus der fünfeckigen Restplatte soll durch Schnitte parallel zu den Seiten des ursprünglichen Rechtecks eine möglichst große rechteckige Platte herausgeschnitten werden.

Welche Maße hat diese rechteckige Platte, und wie viel Prozent der ursprünglichen Plattenfläche nimmt sie ein?

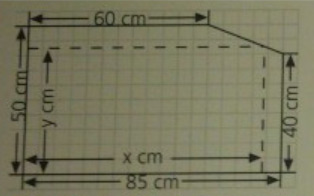
Es soll zwei Wege geben. Einen über den Strahlensatz und einen über eine quadratische Funktion.

Problem beim Finden der Strahlensatzfigur

Answer 1

Ich würde die abgebrochene Ecke über eine lineare Funktion darstellen.


Die Steigung beträgt.

m = (40 - 50) / (85 - 60) = - 0.4


Damit habe ich die Steigung und z.B. den Punkt P(60, 50) und kann darüber die Punkt-Steigungsform aufstellen

f(x) = - 0.4 * (x - 60) + 50 = 74 - 0.4·x

Ich zeichne die Gerade mal gestrichelt ein.


Nun möchte man daraus eine möglichst große Rechtecksfläche machen. Dazu lassen wir einen Punkt über die Gerade fandern und stellen uns dafür einen Funktionsterm auf, welcher den Flächeninhalt des Rechtecks angibt.

A(x) = x * f(x)
A(x) = x * (74 - 0.4·x) = 74·x - 0.4·x^2


Damit die Fläche maximal wird müssen wir die Ableitung gleich null setzen.

A'(x) = 74 - 0.8·x = 0
x = 92.5


Die 92.5 sind nicht mehr im Definitionsbereich von x der ja nur von 0 bis 85 geht. Daher erreichen wir bei 85 unsere maximale Fläche.


Den Rest solltest du jetzt eventuell selber bestimmen können oder?

Hier noch eine Skizze von mir