Wie viele Zentner können auf einem Gerstenboden untergebracht werden?

Question

Auf einem Gerstenboden können bei einer Schütthöhe von 75 cm und einem hl-Gewicht der Gerste 68 kg 525 Ztr. gelagert werden.

Wie viel Ztr. können bei einer Schütthöhe von 100 cm und einem hl-Gewicht von 70 kg untergebracht werden?

Answer 1

 

gegeben ist: Schütthöhe 75cm, hl-Gewicht 68kg, 525 Zentner können gelagert werden.

 

Annahme, wir hätten bei einer veränderten Schütthöhe das gleiche hl-Gewicht: Schütthöhe 100cm, hl-Gewicht 68kg, es können gelagert werden: 525/3*4 Zentner = 700 Zentner.

 

Daraus ergibt sich bei einem hl-Gewicht von 70kg:

Schütthöhe 100cm, hl-Gewicht 70kg, es können gelagert werden: 700 Zentner/68*70 ≈ 720,588 Zentner.

 

Besten Gruß

Comments

Ich habe im Gegensatz zu JotEs nicht mit einem Kegel gerechnet, sondern mit einem Quader als Behälter. Aus diesem Grunde weicht mein Ergebnis von dem seinen sehr stark ab.

Ein "Schüttkegel" war mir bis dato unbekannt :-)

---

Einwand: Das Volumen von Schüttkegeln verändert sich nicht proportional zu deren Höhe. Daher darfst du nicht einfach die Masse des ersten Schüttkegels mit dem Höhenverhältnis der beiden Kegel multiplizieren um auf die Masse des zweiten Kegels zu kommen.

EDIT: Habe deinen Kommentar gelesen. So gesehen hast du natürlich recht. Es kommt jetzt darauf an, wie die Aufgabenstellung gemeint war ...

---

@JotEs:

Danke Dir! Deine Lösung ist natürlich anspruchsvoller - kommt vielleicht wirklich auf die Klassenstufe an, wie die Aufgabenstellung gemeint war :-)

Answer 2

Für das Volumen eines Schüttkegel gilt:

V = ( 1 / 3 ) * π * r ² * h

Somit gilt für das Volumen des ersten Schüttkegels:

V₁ = ( 1 / 3 ) * π * r₁² *  h₁

und für das Volumen des zweiten Schüttkegels:

V₂ = ( 1 / 3 ) * π * r₂² * h₂

und daher für das Verhältnis der beiden Volumina:

V₂ / V₁ = ( ( 1 / 3 ) * π * r₂² * h₂ ) / ( ( 1 / 3 ) * π * r₁² *  h₁ )

= ( r₂² * h₂ ) / ( r₁² * h₁ )

Setzt man die bekannten Höhen ein so erhält man:

V₂ / V₁ = ( r₂² * 100 ) / ( r₁² * 75 )

<=> V₂ / V₁ = ( 4 / 3 ) * ( r₂ / r₁ ) ²

 

Betrachtet man nun die beiden Kegel so:

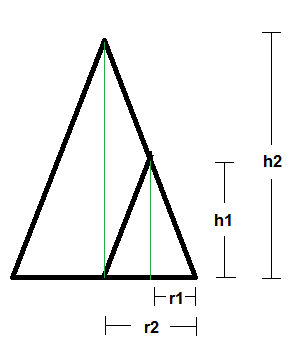
so erkennt man, dass nach dem zweiten Strahlensatz gilt:

r₁ / h₁ = r₂ / h₂

<=> r₂ / r₁ = h₂ / h₁

Die Höhen sind bekannt, also setzt man ein:

r₂ / r₁ = 100 / 75 = 4 / 3 

Dies setzt man nun in die oben fett gesetzte Formel für das Verhältnis der Volumina ein und erhält damit:

V₂ / V₁ = ( 4 / 3 ) * ( r₂ / r₁ ) ² = ( 4 / 3 ) * ( 4 / 3 ) ² = ( 4 / 3 ) ³

<=> V₂ =  ( 4 / 3 ) ³ * V₁

Das Volumen des größeren Kegels ist also ( 4 / 3 ) ³ mal so groß wie das des kleineren Kegels.

Das Volumen des kleineren Kegels kann aus den Angaben der Aufgabenstellung berechnet werden: 

100 l = 68 kg = ( 68 / 50 ) Ztr

<=> 1 Ztr. = 100 * 50 / 68 l

<=> 525 Ztr = 525 * 5000 / 68 ≈ 38602,94 l

Das Volumen des größeren Kegels ist das ( 4 / 3 ) ³ - fache dieses Volumens, also:

V₂ = 38602,94 * ( 4 / 3 ) ³ ≈ 91503,27 l

und dieses Volumen hat bei einer Dichte von 70 kg / 100 l = 0,7 kg / l eine Masse von

91503,27 l * 0,7 kg/l ≈  64052,29 kg = 1281,05 Ztr.