Liebes Forum,
zur Zeit beschäftige ich mich mit partiellen Differentialgleichungen bzw. deren Lösungen.
In der Vorlesung haben wir uns mit partiellen DGl 1. und 2. Ordnung in zwei Dimensionen (Ort (x) und Zeit (t)) unterhalten.
Beispiel:
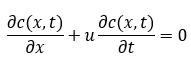
Als Produktansatz wähle ich:
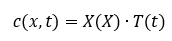
Wenn ich diesen in meine p-DGl. einsetze erhalte ich:
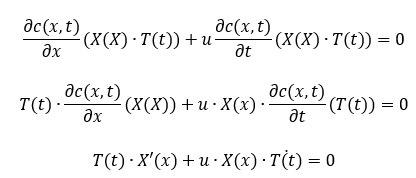
Anschließend trenne ich die Variablen, indem ich durch X(x) und T(t) dividiere:
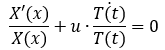
Im nächsten Schritt wähle ich, da beide Seiten konstant sind die Separationskonstante k, indem ich die zeitabhängige Funktion auf die rechte Seite bringe:
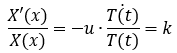
Dadurch erhalte ich zwei gewöhnliche DGl 1. Ordnung, die ich lösen kann.
Mein Problem:
Wie gehe ich vor, wenn ich nicht nur 2 Dimensionen, sondern 3 Dimensionen habe?
Hierzu haben wir folgende Aufgabe bekommen:
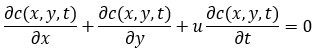
Gleiches Schema:
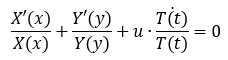
Aber wie wähle ich nun die Separationskonstante?
Unser Professor meinte, wir sollen für jeden Ausdruck eine eigene Konstante einführen und diese sollen in Summe wieder 0 ergeben. Ich habe mich für k, l und m entschieden.
k + l + m = 0
k = - l - m
Für die Ortsfunktion wäre dies also:
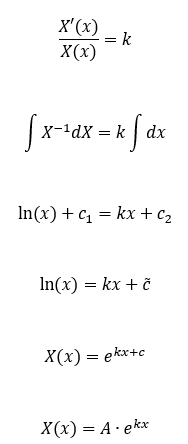
Wenn ich diesen Vorgang für Y und T wiederhole komme ich am Ende auf die allgemeine Lösung:
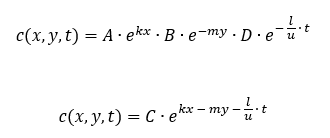
Die Konstanten A, B und D habe ich zu C zusammengefasst. Für die e-Funktionen gilt das Potenzgesetz.
Meine Fragen wären nun:
1.) Kann ich bei mehreren Dimensionen so vorgehen wie beschrieben?
2.) Wie bestimme ich hier die spezielle Lösung?
Ich habe 4 Konstanten (C, k, m und l) habe aber nur 3 Randbedingungen gegeben, da meine DGl nur aus 3 Dimensionen bestand.
Kann ich die Vierte aus
k = -l - m bestimmen?
Über eine Antwort würde ich mich sehr freuen.
Viele Grüße
Suomi :-)