Aufgabe:
Es wird der Serotonin Gehalt im Blut gemessen,vor und nach Zucker Konsum.
Tabelle siehe Bild
Text erkannt:
\begin{tabular}{lllllllll}
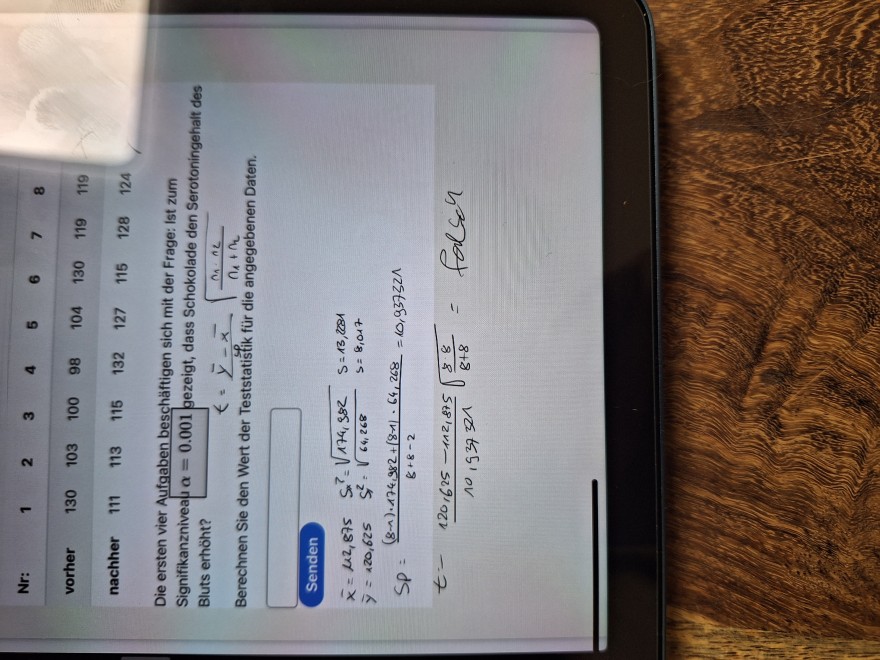
\hline Nr: & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
\hline vorher & 130 & 103 & 100 & 98 & 104 & 130 & 119 & 119 \\
nachher & 111 & 113 & 115 & 132 & 127 & 115 & 128 & 124
\end{tabular}
Die ersten vier Aufgaben beschäftigen sich mit der Frage: Ist zum Signifikanznivea \( \alpha=0.001 \) gezeigt, dass Schokolade den Serotoningehalt des Bluts erhöht?
\( t=\bar{y}-\bar{x} \sqrt{\frac{n_{1} \cdot n_{2}}{n_{1}+n_{2}}} \)
Berechnen Sie den Wert der Teststatištik für die angegebenen Daten.
Senden
\( \begin{array}{l} \bar{x}=\mu 2,875 \quad S_{x}^{2}=\sqrt{174,982} \quad s=13,281 \\ \bar{y}=120,625 \quad S^{2}=\sqrt{64,268} \quad s=8,017 \\ S P=\frac{(8-1) \cdot 174,982+(8-1) \cdot 64,268}{8+8-2}=10,937321 \\ t=\frac{120,625-112,875}{10,937321} \sqrt{\frac{8 \cdot 8}{8+8}}= \end{array} \)
Problem/Ansatz:
Auf dem Bild ist mein Ansatz.. aber die Lösung ist falsch leider...
Und dann soll man noch den p Wert berechnen.. ist dazu die Formel
1-F(-t)