Flächeninhalt von Parabel bestimmen (Benötigt um den Schwerpunkt zu bestimmen)

Question

Aufgabe:

Flächeninhalt von Parabel bestimmen (Benötigt um den Schwerpunkt zu bestimmen)

Problem/Ansatz:

Hallo zusammen,

ich habe folgende Aufgabe und komme nicht weiter:

Ich soll von dieser Fläche den Schwerpunkt berechnen und benötige dafür den Flächeninhalt der Parabel:

https://www.matheretter.de/rechner/geozeichner?draw=polygon(0%7C0%202%7C0%205%7C3%200%7C3)%0Abogen(3%7C3%201%7C3%20-2)%7Bff0000%7D%0Atext(1%7C4%20%22l%C3%A4ngen%20in%20a%22)%7Bb17%7D%0A%0Astrecke(1%7C3%203%7C3)&scale=10

alle größen sind in "a" gegeben (Parabel also 2a breit und 2a hoch).

Ich habe bereits versucht das Integral zu bestimmen, komme jedoch dann immer auf ein "a^3" als Lösung und kann damit dann nicht weiter den Schwerpunkt berechnen. Als f(x) der Funktion hab ich mit f(x)=2*(x^2) gerechnet.

Danke schonmal im voraus.

Comments

Um welche Fläche geht es?

---

Man soll den Schwerpunkt der blauen Fläche, ohne die der roten Parabel berechnen.

Die Fläche des Trapezes kriege ich hin. Die rote Parabel (auf dem link zu sehen) bereitet mir aber Probleme, da ich immer eine Potenz dritten Grades bekomme und damit nicht den Schwerpunkt bestimmen kann.

---

Um welche Fläche geht es?

um diese (die rot umrandete):

~draw~ polygon(0|0 2|0 5|3 0|3);bogen(3|3 1|3 -2){ff0000};text(1|4 "längen in a"){b17};strecke(1|3 3|3);zoom(5) ~draw~

---

Flächeninhalt von Parabel bestimmen

Eine Parabel hat keinen Flächeninhalt.

---

Meine Idee war es halt zuerst das Quadrat zu berechnen (also 2a*2a = 4a^2) und davon dann anschließend das Integral von -a bis a der Parabel zu berechnen und abzuziehen.

Was meinst du mit "eine Parabel hat keinen Flächeninhalt"?

---

Was meinst du mit "eine Parabel hat keinen Flächeninhalt"?

Genau das, was ich geschrieben habe.

Eine Parabel ist sehr lang aber sehr dünn, darum hat sie keinen Flächeninhalt.

---

Parabel also 2a breit und 2a hoch

so ein Parabelsegment nimmt immer 2/3 der Fläche des umhüllenden Parallelogramms ein (hier ist es ein Rechteck). D.h. in diesem Fall ist die Fläche \(F_P\) des Parabelsegements$$F_P = \frac{2}{3} \cdot 2a \cdot 2 a = \frac{8}{3}a^2$$

---

zur Kontrolle:

Answer 1

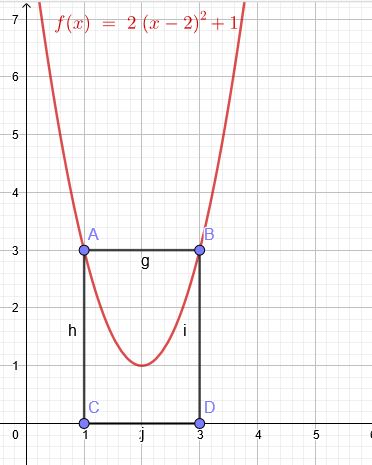
Inhalt des Rechtecks A,B,C,D \(A=6FE\)

Fläche unter der Parabel

\(f(x)=2*(x-2)^2+1=2x^2-8x+9\)

\(A=\int\limits_{1}^{3}(2x^2-8x+9)dx=[\frac{2}{3}x^3-4x^2+9x]_{1}^{3}=[18-36+27]-[\frac{2}{3}-4+9]=\frac{10}{3}F E\)

gesuchter Flächeninhalt in der Parabel:

\(A=6-\frac{10}{3}=\frac{8}{3}F E\)

Comments

FE steht für Flächeneinheit?

Also kann ich das einfach so berechnen und am Ende mein a^2 als Einheit eintragen ohne das es da Probleme gibt? → (8/3) * a^2 also als Lösung?

Answer 2

Offenbar geht es um diesen Flächeninhalt:

Von Flächeninhalt des Trapezes, den du ja schon berechnet hast, musst du              \( 6 - \int\limits_{1}^{3} \) (2(x-2)²+1)dx subtrahieren.

Comments

Berechne ich dann nicht die gesamte Fläche unter der Parabel von 1 bis 3?

Ich brauche doch die Fläche der Parabel und muss diese dann von dem Trapez abziehen.

---

Ich habe meine Antwort noch einmal nachgebessert.