Im Mai 2013 erschien in der Mathelounge die Frage: „Wer hat die Gleichung erfunden, oder wer weiß über die Geschichte der Gleichung Bescheid?“
Eine Antwort lautete damals: „Ich bezweifle stark, dass man hier eine Person nennen kann. Ich denke vielmehr, dass das eine Entwicklung war, die sich über sehr lange Zeiträume hingezogen hat. Ich vermute ebenfalls, dass das sehr weit zurück geht. [Gleichungen waren] mit Sicherheit bei den Griechen bekannt; bei den Ägyptern und Chinesen ist es auch fast sicher anzunehmen.“
Diese Antwort nennt Vermutungen und Überzeugungen, die sich zum Teil als falsch herausstellen. Hier soll eine neue Antwort aus diese alte Frage versucht werden:
Unter einer Gleichung verstehen wir heute eine Zeichenkette aus Zahlzeichen, Rechenzeichen Platzhaltern und einem Gleichheitszeichen. Die Geschichte der Mathematik nennt von diesen Zeichen die Zahlzeichen als die ältesten. Alle anderen Bestandteile einer Gleichung sind neueren Datums. Darunter sind die Zeichen für Platzhalter und auch das Gleichheitszeichen die Jüngsten. Frühe Kulturen haben alles, was sie zur Mathematik ihrer Zeit wussten, in den Worten ihrer Sprache – ergänzt durch geometrische Darstellungen – ausgedrückt. Das betraf auch Aufgabenstellungen und Lösungswege dazu. Von den Sumerern ist eine Tontafel erhalten, welche die Abbildung eines Quadrats, seiner Diagonalen und einige sumerische Zahlzeichen zeigt. In unserer heutigen Darstellung gibt diese Tontafel die Gleichung √2=1,414214 wieder. Die Sumerer kannten also Identitäten. Man kann aber nicht sagen, dass die Kenntnis von Identitäten den Anfang der Geschichte der Gleichungen markiert. Wo dieser Anfang genau liegt, ist vielleicht dann fixierbar, wenn man die Einführung eines Gleichheitszeichens zum Start einer Geschichte der Gleichungen erklärt. Descartes (1596 – 1650) verwendete ein Zeichen, dass etwa so aussah. 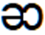
Man darf vermuten, dass ihn die Anfangsbuchstaben ae des lateinischen Wortes für Gleichung (um 180° gedreht) zu dieser Schreibweise angeregt hatten. Leibniz (1646 – 1716) übernahm dann für den deutschen Raum aus England das heute noch gebräuchliche Zeichen = für die Gleichheit.
Der Begriff der Gleichung beinhaltet im weitesten Sinne auch solche Zusammenhänge, die heute in Form einer Gleichung dargestellt werden, nicht aber in früheren Phasen der Geschichte der Mathematik. Ein Beispiel aus der sumerischen Mathematik hierzu wurde oben genannt. Die griechische Mathematik kannte zum Beispiel die Frage nach den Seitenlängen eines Rechtecks, dessen halber Umfang sowie dessen Fläche bekannt waren. Die Griechen fanden zu diesem Problem eine geometrische Lösung, ohne eine einzige Gleichung niederzuschreiben. Auch der Rechenmeister Adam Riese (1492/93 bis 1559) schrieb in seinem ‚Rechenbüchlin‘ zahlreiche Fragestellungen aus dem Alltags- und Berufsleben auf, die heute mit Hilfe von Gleichungen gelöst werden. Da Riese die Notation als Gleichung nicht kannte, gab er den gegebenen Größen eine Anordnung und beschrieb, wie und in welcher Reihenfolge diese zur weiteren Ermittlung der Unbekannten zu nutzen seien. Selbst die fundamentale Idee des funktionalen Zusammenhangs existierte sehr lange vor der Erfindung des Konzeptes der Gleichung. Nikolaus von Oresme ordnete bereits Mitte des 14. Jahrhunderts jeder ‚quantitas‘ eine ‚qualitas‘ zu, um Kegelschnitte zu beschreiben.
In der Mathematik der Antike, der arabischen Mathematik und der europäischen Mathematik bis zum Ende des 16. Jahrhunderts wurden Gleichungen ausschließlich in Textform gegeben und gelöst. Dieses Faktum sowie weitere Fakten aus der Geschichte der Gleichungen findet man unter
Gleichungen, Wissenswertes und Historisches in Mathematik | Schülerlexikon | Lernhelfer.