Darstellungsmatrix mit Funktionenraum

Question

Text erkannt:

Wir betrachten den von der Basis \( B: b_{1}: \mathbb{R} \rightarrow \mathbb{R}: t \mapsto \cos (t), b_{2}: \mathbb{R} \rightarrow \mathbb{R}: t \mapsto \sin (t) \) aufgespannten Funktionenraum \( V=\left\{\alpha b_{1}+\beta b_{2} \mid \alpha, \beta \in \mathbb{R}\right\} \subseteq \mathcal{C}^{0}(\mathbb{R}) \).
Bestimmen Sie die Darstellungsmatrix \( { }_{B} \rho_{B} \) der linearen Abbildung \( \rho: V \rightarrow V: f \mapsto \rho(f) \), wobei die Abbildung \( \rho(f): \mathbb{R} \rightarrow \mathbb{R} \) durch \( (\rho(f))(t)=f\left(t-\frac{3}{2} \pi\right) \) gegeben ist.

Aufgabe:

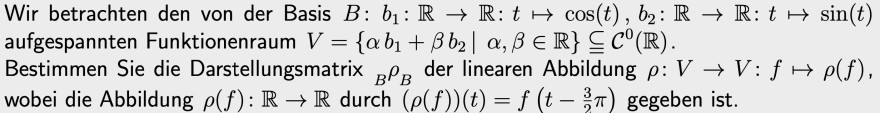
Text erkannt:

Wir betrachten den von der Basis \( B: b_{1}: \mathbb{R} \rightarrow \mathbb{R}: t \mapsto \cos (t), b_{2}: \mathbb{R} \rightarrow \mathbb{R}: t \mapsto \sin (t) \) aufgespannten Funktionenraum \( V=\left\{\alpha b_{1}+\beta b_{2} \mid \alpha, \beta \in \mathbb{R}\right\} \subseteq \mathcal{C}^{0}(\mathbb{R}) \).
Bestimmen Sie die Darstellungsmatrix \( { }_{B} \rho_{B} \) der linearen Abbildung \( \rho: V \rightarrow V: f \mapsto \rho(f) \), wobei die Abbildung \( \rho(f): \mathbb{R} \rightarrow \mathbb{R} \) durch \( (\rho(f))(t)=f\left(t-\frac{3}{2} \pi\right) \) gegeben ist.

Problem/Ansatz:

Ich brauche Hilfe beim Lösen dieser Aufgabe.

Wenn man in b1 und b2 vor dem t die -3pie/2 einsetzt ergibt sich b1=-sin(t) b2=cos(t) wie ich daraus jetzt nun die Darstellungsmatrix bilden soll.

Answer 1

Die Darstellungsmatrix \(_{B_1}\rho_{B_2}\) hat als Spalten die Koordinatenvektoren bezüglich \(B_2\) der Bilder der Vektoren aus \(B_1\).

Der erste Vektor aus \(B_1\) ist \(\sin\). Es ist

        \(\rho(\sin): V\to V,\ t\mapsto \sin\left(t-\frac{3}{2}\pi\right)\).

Laut Additionstheorem ist

        \(\begin{aligned} \sin\left(t-\frac{3}{2}\pi\right) & =\sin\left(t\right)\cos\left(\frac{3}{2}\pi\right)-\cos\left(t\right)\sin\left(\frac{3}{2}\pi\right)\\ & =\cos\left(\frac{3}{2}\pi\right)b_{1}-\sin\left(\frac{3}{2}\pi\right)b_{2}\text{.} \end{aligned}\)

Die erste Spalte von \(_{B}\rho_{B}\) lautet also \(\left(\begin{smallmatrix}\cos\left(\frac{3}{2}\pi\right)\\-\sin\left(\frac{3}{2}\pi\right)\end{smallmatrix}\right)\).

Answer 2

Wir haben

\((\rho(b_1))(t)=\cos(t-3/2\pi)=\cos(t+\pi/2)=-\sin(t)=0\cdot b_1(t)+(-1)\cdot b_2(t)\) und

\((\rho(b_2))(t)=\sin(t+\pi/2)=\cos(t)=1\cdot b_1(t)+0\cdot b_2(t)\).

Das ergibt die Darstellungsmatrix

\(\left(\begin{array}{rr}0&1\\-1&0\end{array}\right)\).