Ist die Funktion im Nullpunkt stetig?

Question

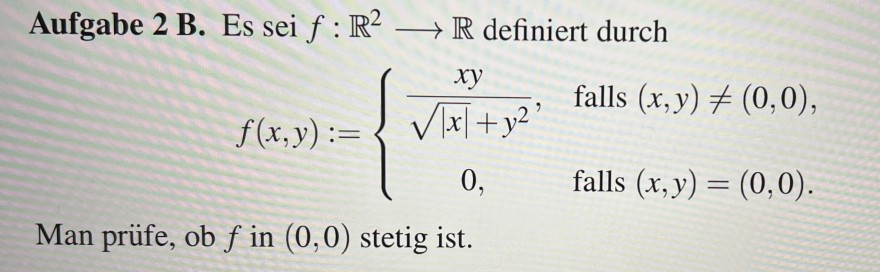
Text erkannt:

Aufgabe 2 B. Es sei $f: \mathbb{R}^{2} \longrightarrow \mathbb{R}$ definiert durch
$f(x, y):=\left\{\begin{array}{cc} \frac{x y}{\sqrt{|x|}+y^{2}}, & \text { falls }(x, y) \neq(0,0), \\ 0, & \text { falls }(x, y)=(0,0) . \end{array}\right.$
Man prüfe, ob $f$ in $(0,0)$ stetig ist.

Meine Vermutung wäre, dass die Funktion stetig wäre. Aber es zu beweisen fällt mir schwer. Ist die eventuell doch nicht stetig?

Answer 1

Wie kann ich das denn jetzt noch beweisen?

$$\left|\frac{xy}{\sqrt{|x|}+y^2}\right|\leq\frac{|x||y|}{\sqrt{|x|}}=\sqrt{|x|}|y|\to 0$$für $(x,y)\to (0,0)$.

Answer 2

Der Funktionswert ist gleich dem Grenzwert für [x.y]→[0,0].

Comments

Danke. Wie kann ich das denn jetzt noch beweisen?