Hallo Valeria,
Vektoren sind wie Pfeile, wobei ein Pfeil immer in die selbe Richtung zeigt und immer die selbe Länge hat. Aber(!) er darf beliebig verschoben werden, Nehmen wir als mal drei Stück:
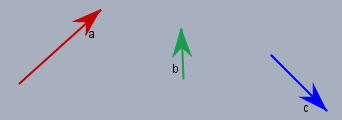
so - jetzt ist gefargt nach ...
a) u= 0.5 a + 2b
... \(u\)! Wenn vor dem Vektor eine Zahl steht, so ändert sich seine Länge (außer da steht eine \(1\)). Bei \(0,5\) soll er halb so lang sein, und bei \(2\) doppelt so lang. Und ein Plus-Zeichen zwischen dern Vektoren bedeutet, dass sie aneinander gehängt werden sollen. Verschieben darf man immer - also gibt das:
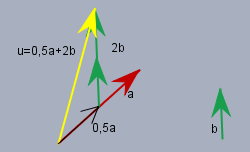
Ich habe den roten Vektor \(a\) halbiert, das gibt das schwarze Stück und an diese Hälfte das Doppelte des Vektors \(b\) dran gehängt. Und das Ergebnis vom Anfang von \(0,5a\) bis zum Ende von \(2b\) ist der gesuchte Vektor \(u\) (gelb).
Das geht auch mit dreien ...
b) v= 2c + 0.5 a - 3/4 a
... eigenlich nur zwei, denn \(0,5 - 1/4 = -1/4\) - also \(v = 2c - 1/4a\). Ist der Faktor vor dem Vektor negativ, so zeigt er in die Gegenrichtung
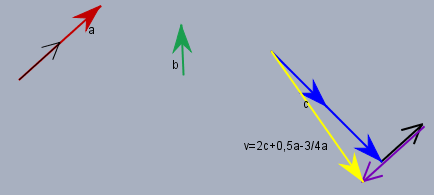
Der lilane Vektor hat die Länge von \(3/4\) von \(a\) und zeigt in die Gegenrichtung, wegen dem Minus davor. Und \(0,5a - 3/4a\) gibt eine Vektor, der \(1/4\) der Länge von \(a\) hat und in die Gegenrichtung von \(a\) zeigt, eben weil das Ergebnis von \(0,5-3/4=-1/4\) negativ ist.
Falls Du noch Fragen hast, so melde Dich bitte!
Gruß Werner