Aufgabe:
Ziel dieser Aufgabe ist es, die Weibull-Verteilung mit Parametern \( \lambda, k>0 \) in Maxima zu modellieren. Diese lässt sich, beispielweise, durch folgende Umwandlung zu charakterisieren:
\( W=-\frac{1}{\lambda^{k}} \ln (U), \)
wo \( U \) eine \( \mathcal{U}_{[0,1]} \)-verteilte Zufallsvariable (Gleichverteilung auf \( [0,1] \) ) ist, und \( W \) eine Weibull-verteilte Zufallsvariable mit Parametern \( \lambda, k>0 \) ist. Thre Aufgabe ist, mit Hilfe von obiger Formel die empirische Verteilungsfunktion für \( W \) zu erzeugen und sie anschliefend zusammen mit der echten Verteilungsfunktion der Weibull-Verteilung zu visualisieren. Schreiben Sie eine Blockformel weibull, die folgendes tut:
1. Als Eingabe erwartet eine Natürliche Zahl \( n \), eine positive reelle Zahl \( \lambda \) und eine positive reelle Zahl \( k \);
2. Sie erzeugt eine Liste \( T \) der Lange \( n \) von Werten der Weibull-Verteilung mit Parametern \( \lambda, k \);
3. Sie bildet anhand von \( T \) eine empirische Verteilungsfunktion und eine theoretische Verteilungsfunktion für die erwähnte Weibull-Verteilung in einer Graphik ab.
Hinweise: In Maxima gibt der Befehl random \( (f l o a t(a)) \) eine \( \mathcal{U}_{[0, a]} \)-verteilte Zufallsvariable aus. Die empirische Verteilungsfunktion, gegeben Werte \( x_{1}, \ldots, x_{n} \), kann wie folgt bestimmt werden:
\( F_{n}(x)=\frac{1}{n} \sum \limits_{i=1}^{n} \mathbb{1}_{\left\{x_{i} \leq x\right\}} \)
Beispiele der Eingabe und Ausgabe:
Text erkannt:
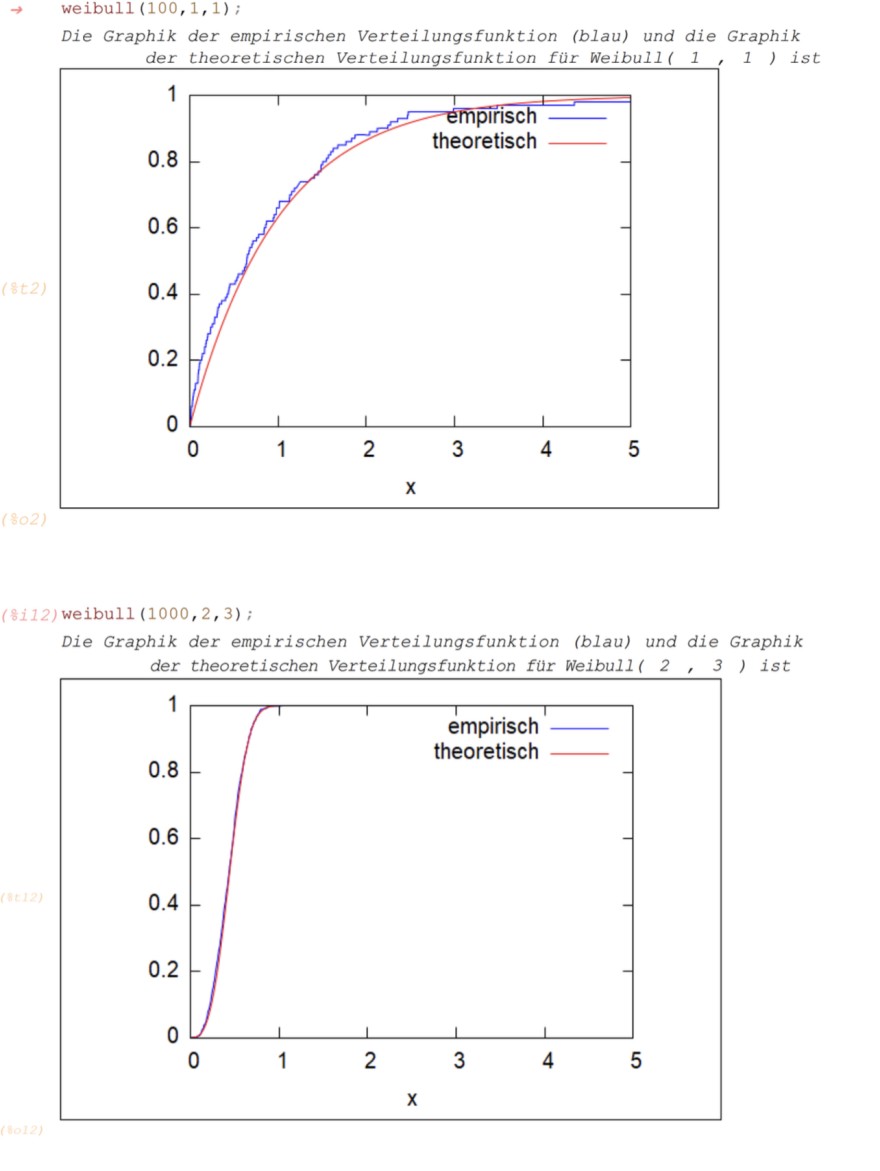
\( \rightarrow \quad \) weibull \( (100,1,1) \);
Die Graphik der empirischen Verteilungsfunktion (blau) und die Graphik der theoretischen Verteilungsfunktion für Weibull( 1, 1 ) ist
\( (802) \)
(8112) weibull \( (1000,2,3) \);
Die Graphik der empirischen Verteilungsfunktion (blau) und die Graphik der theoretischen Verteilungsfunktion für Weibull ( 2, 3 ) ist
Problem/Ansatz:
Die in Maxima eingebauten Befehle für Weibull-Verteilung bzw. empirische Verteilungsfunktion dürfen nicht benutzt werden