Ich suche jemanden der sich mit dem Computerprogramm Maxima auskennt und mir bei folgender Aufgabe helfen kann:
Modellierung von geometrischer Verteilung
Ziel dieser Aufgabe ist es, geometrisch verteilte Zufallsvariable in Maxima zu definieren. Schreiben Sie dazu eine Blockformel \( g e o m \), die folgendes tut:
1. Sie nimmt das Parameter \( p \) der geometrischen Verteilung ein.
2. Es wird überprüft, ob die Eingabe sinnvoll ist. \( p \) muss in \( [0,1] \) liegen. Wenn diese Bedingung nicht erfüllt wird, wird die Fehleranzeige ausgegeben (2P);
3. Es wird die allgemeine Formel für Wahrscheinlichkeitsfunktion \( P(X=k) \) für die geometrisch verteilte Zufallsvariable mit dem eingegebenen Parameter \( p \) ausgegeben (2P);
4. Es wird die Graphik von der Wahrscheinlichkeitsfunktion von \( X \) für \( k=1 \ldots 10 \) gezeichnet (4P).
Vorsicht! Werden Sie die in Maxima eingebauten Funktionen für Verteilungsfunktion/Eigenschaften der geometrischen Verteilung benutzen, wird diese Aufgabe mit 0 Punkten bewertet.
Dazu haben wir auch eine beispielhafte Lösung bekommen:
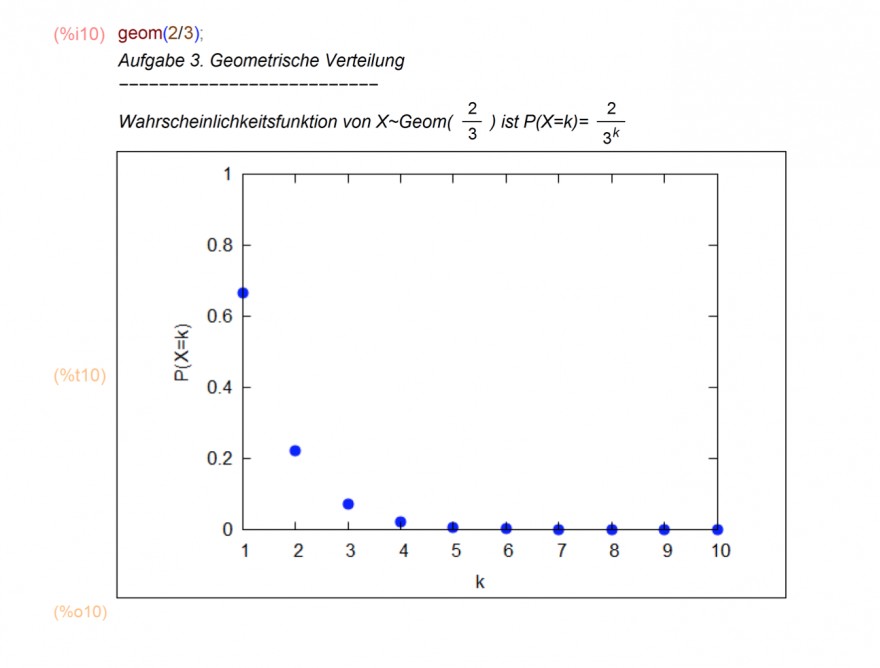
Text erkannt:
(\%i10) geom(2/3); Aufgabe 3. Geometrische Verteilung
Wahrscheinlichkeitsfunktion von \( X \sim \operatorname{Geom}\left(\frac{2}{3}\right) \) ist \( P(X=k)=\frac{2}{3^{k}} \)
(t10)
\( (\% 010) \)
Ich verstehe leider wirklich nur Bahnhof, mit geometrischen Verteilungsfunktionen kenne ich mich eigentlich aus, bzw das Thema habe ich verstanden, nur von Maxima habe ich leider überhaupt keinen Plan und das Internet konnte mir bis jetzt auch nicht weiterhelfen. Bitte kann mir hier jemand helfen ...