Bestimmen Sie die Erwartungswert von X und Y und die Wahrscheinlichkeit P(X≤2,Y=2)

Question

Aufgabe:

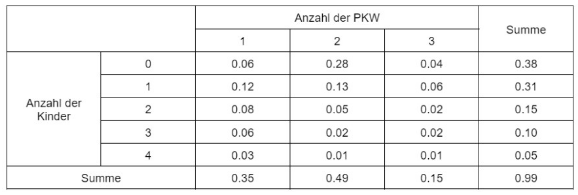
gegeben sei die zweidimensionale Verteilung bezüglich eines Haushalts

Anz. der PKW	1	2	3
Anz. der Kinder
0	0.06	0.28	0.04
1	0.12	0.13	0.06
2	0.08	0.05	0.03
3	0.06	0.02	0.02
4	0.03	0.1	0.1

a) Bestimmen Sie die Randverteilung von X (Anzahl X an Kindern) und Y(Anzahl der PKW)

b)  Bestimmen Sie die Erwartungswerte E(X) und E(Y ) sowie die Wahrscheinlichkeit dafür, dass pro Haushalt genau 2 PKW gefahren werden und höchstens zwei Kinder zum Haushalt zählen.

Problem/Ansatz:

a) habe ich mal so von diesem Forum übernommen wo die Frage aber noch unbeantortet blieb. (Ja, die Gesamtsumme ist 0,99 aber sollte 1 sein. Ich weiß das, aber das was unser Professor uns gibt, damit müssen wir rechnen..)

b) Hier ist meine eigentliche Frage. Ich habe wie folgt E(X)  berechnet:

Ich habe die Randverteilung kommuliert aufgeschrieben, also eine Verteilungsfunktion erstellt und dann quasi mit 0,1,2,.. multipliziert und addiert. Also:

E(X) = 0*0,38 + 1*0,69 + 2*0,84 + 3*0,94 + 4*0,99 = 9,15

Ist das richtig? Auf E(Y) muss ich ja dann weiter nicht eingehen da die Rechnung die selbe ist nur mit anderen Zahlen.

Und die Wahrscheinlichkeit, dass pro Haushalt genau 2 PKW und höchstens zwei Kinder zählen , müsste dann doch sein:

P(X=0,Y=2) + P(X=1,Y=2) + P(X=2,Y=2) = 0,28 + 0,13 + 0,05 =  0,46

Richtig ?

Danke im voraus

Comments

Ja, die Gesamtsumme ist 0,99

Weißt du auch, warum das so ist?

---

Da es eine einfache Stochastik Aufgabe sein soll, nehme ich an, dass es keinen tieferen statistischen Grund hat wieso da 0,99 raus kommt. Vielleicht verrechnet. Keine Ahnung

---

verrat du es mir.... im Endeffekt ist es mir wichtiger ob mein Ansatz und Rechnenmethode korrekt ist

---

Es kommt 0,99 raus, weil die Einträge in der Tabelle gerundet sind.

Beispiel. Auf die Frage, ob sie mit mir ausgehen würden, antworten 24 Frauen mit Ja, 123 Frauen mit Vielleicht und 853 Frauen mit Nein. Rundet man die relativen Häufigkeiten auf zwei Nachkommastellen, dann bekommt man als Summe 0,02+0,12+0,85=0,99.

Rundet man nicht, dann täuscht das Ergebnis eventuell eine Ganauigkeit vor, die angesichts der Stichprobengröße nicht angebracht ist.

---

Danke für den Hinweis! Sind die anderen Ansätze korrekt?

Lg Würstl

Answer 1

E(X) = ... = 9,15

Das kann nicht stimmen, weil keine der Familien mehr als 4 Kinder hat und 4 kleiner als 9,15 ist.

Als mögliche Kinderanzahl treten Zahlen von 0 bis 4 auf, also liegt auch der Erwartungswert in diesem Bereich.

Ich habe die Randverteilung kommuliert aufgeschrieben,

Nicht kummulieren.

Die Formel besagt ja

        E(X) = x₁ · P(X=x₁) + x₂ · P(X=x₂) + ...

Wenn du kumulierst, dann berechnset du

        x₁ · P(X≤x₁) + x₂ · P(X≤x₂) + ...

Comments

Das heißt die Verteilungsfunktion muss nicht kommuliert aufgeschrieben werden?

Oder doch und den Erwartungswert aber nicht anhand der Kommulierten Werte  berechnen?

---

Die Verteilungsfunktion ist per Definition kumuliert, egal wie du sie aufschreibst.

Aber der Erwartungswert ist nicht mittels der Verteilungsfunktion definiert, sondern mittels der Wahrscheinlichkeitsfunktion a.k.a Zähldichte.

Die Verteilungsfunktion bekommst du, indem du die Werte der Wahrscheinlichkeitsfunktion kumulierst. Aber, wie gesagt, die Verteilungsfunktion wird zur Berechnung des Erwartungswertes nicht verwendet.