Aufgabe:
Normalvektor und skalares Produkt
Problem/Ansatz:
Text erkannt:
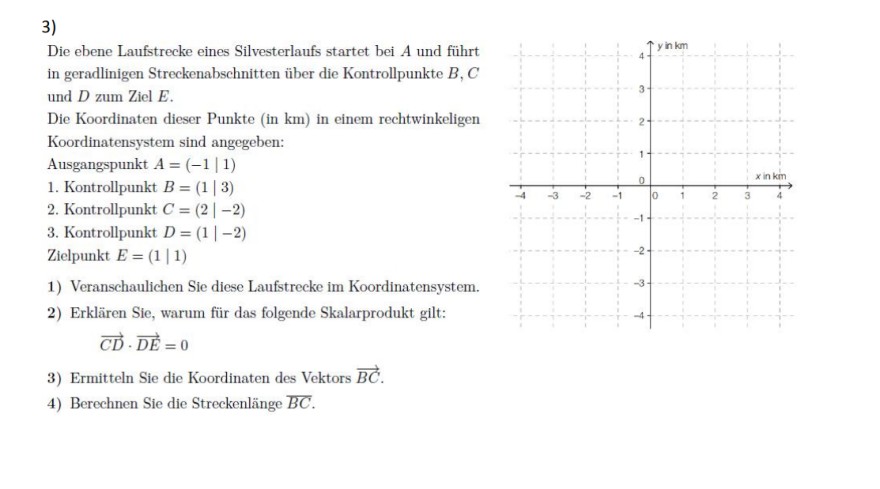
3)
Die ebene Laufstrecke eines Silvesterlaufs startet bei \( A \) und führt in geradlinigen Streckenabschnitten über die Kontrollpunkte \( B, C \) und \( D \) zum Ziel \( E \).
Die Koordinaten dieser Punkte (in \( \mathrm{km} \) ) in einem rechtwinkeligen Koordinatensystem sind angegeben:
Ausgangspunkt \( A=(-1 \mid 1) \)
1. Kontrollpunkt \( B=(1 \mid 3) \)
2. Kontrollpunkt \( C=(2 \mid-2) \)
3. Kontrollpunkt \( D=(1 \mid-2) \)
Zielpunkt \( E=(1 \mid 1) \)
1) Veranschaulichen Sie diese Laufstrecke im Koordinatensystem.
2) Erklären Sie, warum für das folgende Skalarprodukt gilt:
\( \overrightarrow{C D} \cdot \overrightarrow{D E}=0 \)
3) Ermitteln Sie die Koordinaten des Vektors \( \overrightarrow{B C} \).
4) Berechnen Sie die Streckenlänge \( \overline{B C} \).