Berechnen Sie den Flächeninhalt des Dreiecks DEF und das Volumen des Prismas ABCDEF

Question

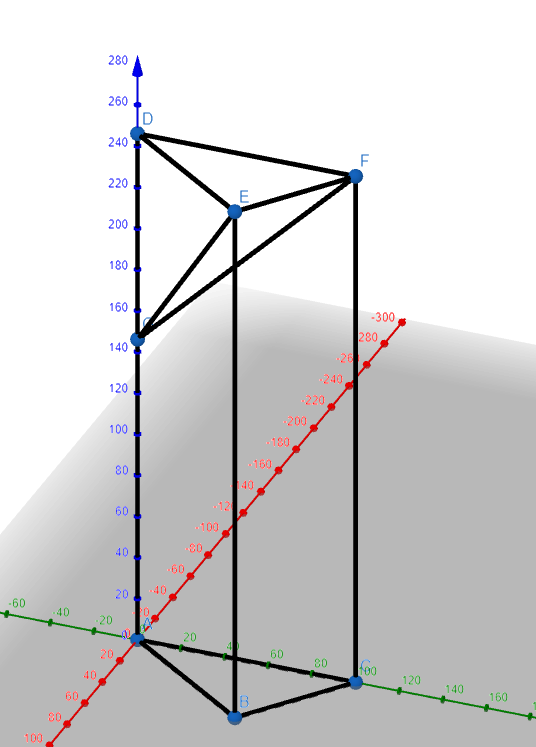
Aufgabe:

In einem kartesischen Koordinatensystem sind die Punkte A(0|0|0), B, C(0|100|0) D(0|0|146), E(48|64|246) und F(0|100|246) sowie der Punkt G(0|0|146) gegeben.

a) Der in der Abbildung dargestellte Körper ABCDEF ist ein Dreieckiges Prisma .

(1) Gebe die Koordinaten des Punktes B an.

Für a≥0 ist der Punkt Ga(0|0|a) gegeben.

(2) Zeigen Sie, dass das Dreieck GaEF für jedes a≥0 im Punkte E rechtwinklig ist.

(3) Der Punkt Ga soll die Strecke AD im Verhältnis 2:1 teilen.

Gebe ein a≥0 so an, dass Ga diese Bedingung erfüllt.

(4) Für a=246 gilt Ga=D

Berechnen Sie den Flächeninhalt des Dreiecks DEF und das Volumen des Prismas ABCDEF

Problem/Ansatz:

Bei a (1) habe ich für B den Punkt B=(48|64|0) heraus.

Bei 2-4 komme ich leider nicht weiter. Daher bitte ich um eure Hilfe

Beste grüße Milan

Answer 1

Wenn zwischen zwei Vektoren ein rechter Winkel sein soll, muss ihr Skalarprodukt 0 sein.

Bilde \(\overrightarrow{EG}\) und \(\overrightarrow{EF}\) und berechne deren Skalarprodukt.

Comments

Hallo, danke für deine Antwort. Worauf ist sie bezogen. (2) (3) oder (4). Ich brauche leider bei allen Hilfe? Grüsse

---

Hallo, danke für deine Antwort. Worauf ist sie bezogen. (2) (3) oder (4). Ich brauche leider bei allen Hilfe?

In nur einer Teilaufgabe spielt Rechtwinkligkeit eine Rolle. Ich nehme die sich in dieser Rückfrage zeigende Denkfaulheit zum Anlass, mich aus der kompletten Aufgabe zurückzuziehen.

---

Nachtrag: Besonders dreist finde ich, dass du den Zusammenhang von Skalarprodukt und Rechtwinkligkeit schon kennst:

https://www.mathelounge.de/1037203/zeigen-beiden-dachstreben-rechts-keinen-rechten-einschliessen

Fazit:

Zukünftige Beiträge von dir - ohne mich.

Answer 2

1) Gebe die Koordinaten des Punktes B an.

B(48 | 64 | 0)

2) Für a ≥ 0 ist der Punkt Ga(0 | 0 | a) gegeben. Zeigen Sie, dass das Dreieck GaEF für jedes a ≥ 0 im Punkte E rechtwinklig ist.

EGa·EF = [-48, -64, a - 246]·[-48, 36, 0] = 0

3) Der Punkt Ga soll die Strecke AD im Verhältnis 2:1 teilen. Gebe ein a ≥ 0 so an, dass Ga diese Bedingung erfüllt.

Ga = [0, 0, 0] + 2/3·[0, 0, 246] = [0, 0, 164] → a = 164

4) Für a = 246 gilt Ga = D Berechnen Sie den Flächeninhalt des Dreiecks DEF und das Volumen des Prismas ABCDEF

A_DEF = 1/2·|[48, 64, 0] ⨯ [0, 100, 0]| = 2400

V = A_DEF·h = 2400·246 = 590400