Aufgabe Stochastik:
Seien \( X \) und \( Y \) zwei unabhängige, gleichverteilte Zufallsvariablen, \( X \) über dem reellen Intervall \( |-2,2| \) und \( Y \) über dem reellen Intervall \( \mid-1,1] \). Es sei \( Z=|X-Y| \) der Absolutbetrag der Differenz aus \( X \) und \( Y \).
a) Betrachten Sie \( Z \) als eine Zufallsvariable über dem Rechteck \( [-2,2] \times[-1,1] \) und bestimmen Sie die Verteilungsfunktion \( F_{z} \) und die Dichtefunktion \( f_{z} \).
b) Bestimmen Sie den Erwartungswert \( E(\underline{Z}) \).
c) Bestimmen Sie die Wahrscheinlichkeit \( \operatorname{Pr}(Z \geq 2) \). Welche obere Abschätzung dieser Wahrscheinlichkeit ergibt sich aus der Markov-Ungleichung?
Hinweise:
$$ \text { - Kontrollergebnis: } f_{z}(x)=\left\{\begin{array}{ll} 0 & \text { falls } x<0 \text { uder } x>3 \\ \frac{1}{2} & \text { fulls } 0 \leq x<1 \\ \frac{3-z}{4} & \text { falls } 1 \leq x \leq 3 \end{array}\right. $$
- Zur Lösung von a) können Sie die folgende Skizze verwenden und vervollständigen. Die Fläche eines Parallelogramms ist das Produkt aus einer Grundseite und der Höhe darauf.
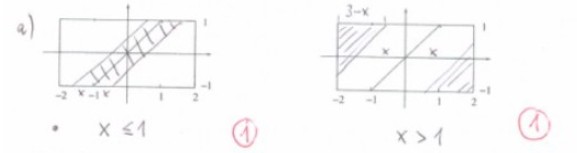
x ≤ 1
\( \operatorname{Pr}(z \leq x)=\frac{2 \cdot 2 x}{8}=\frac{x}{2} \)
Zähler = Fläche der Parall.
Nenner = Gesamtfläche
x > 1
\( \operatorname{Pr}(z \leq x)=1-\operatorname{Pr}(z \geqslant x) \)
\( =1-\frac{(3-x)^{2}}{8}=\frac{-x^{2}+6 x-1}{8} \)
Zähler = Fläche der zwei Dreiecke
\( F_{z}(x)=\left\{\begin{array}{ll}0 & \text { falls } x<0 \\ x / 2 & \text { falls } 0 \leq x \leq 1 \\ \frac{\left(-x^{2}\right)+6 x-1}{8} & \text { falls } 1<x \leq 3 \\ 1 & \text { falls } x>3\end{array}\right. \)
Ansatz:
Ich weiß nicht wie er auf folgende Verteilungsfunktion gekommen ist und warum er die Fälle <1 und ≥ 1 betrachtet hat und wie er auf die Skizzen gekommen ist.